Home · Book Reports · 2018 · Cryptography and Network Security Principles and Practice

designates my notes. / designates important.

Thoughts

The first half of the book, the cryptography was interesting and why I read the book. The latter half, network protocols and such was old-hat for me. That said, I would strongly recommend this book to anyone interested in either cryptography or network security.

Ample, but not detailed, mathematical foundations are provided, allowing anyone without the prerequisite math skills to understand the entire book, provided you are willing to roll up your mental sleeves. The elliptical parts are quite difficult, but the rest is infinitely approachable by a novice.

It also covers the various forms ciphers can take, block, stream, etc. Random and pseudo random number generators are discussed. Public and private key systems are elaborated.

There are TONS of illustrations to help you visualize the algorithms and communication routines. There are also many examples, starting from the most basic shift ciphers all the way to DES, AES, and RSA. Hashing is also covered in great detail with the aforementioned illustrations and examples.

Enough detail is given that you can easily implement the algorithms in a programming language of your choosing. I built a number of python based toy examples for things like the euclidean algorithm, the Miller-Rabin prime test, and an RSA implementation among other things. I would strongly suggest anyone interested in learning cryptography to implement as many of the algorithms as you can, from scratch. The amount you learn doing this far exceeds what you would get simply trying to absorb the book.

It really is a well rounded book.

Code

Here are links to the python programs I wrote, but be warned these are not debugged and more of proof of concepts to facilitate understanding. Do not use them for anything more than learning.

• auth.py
• caesar_cipher.py
• client.py
• crt.py
• euclide2.py
• gcd.py
• miller-rabin_prime_test
• rsa.py
• sbox_gen.py
• transpose.py

Books

• Read all of the classic papers cited in the Recommended Reading section for this chapter, available at the Author Web site at WilliamStallings.com/Cryptography. The papers are available at box.com/Crypto7e.

• Dorothy Sayers’s Have His Carcase (fiction)

Table of Contents

• 01: Computer and Network Security Concepts
• 02: Introduction to Number Theory
• 03: Classical Encryption Techniques
• 04: Block Ciphers and the Data Encryption Standard
• 05: Finite Fields
• 06: Advanced Encryption Standard
• 07: Block Cipher Operation
• 08: Random Bit Generation and Stream Ciphers
• 09: Principles of Public-Key Cryptosystems
• 10: Other Public-Key Cryptosystems
• 11: Cryptographic Hash Functions
• 12: Message Authentication Codes
• 13: Digital Signatures
• 14: Key Management and Distribution
• 15: User Authentication
• 16: Network Access Control and Cloud Security
• 17: Transport-Level Security
• 18: Wireless Network Security
• 19: Electronic Mail Security
• 20: IP Security

· 01: Computer and Network Security Concepts

page 010:

page 21:

• CIA triad = confidentiality, integrity, availability

page 23:

• To this triad add authenticity and accountability

page 27:

• Active attacks can be classified as: masquerade, replay, modification of messages, and denial of service.

page 030:

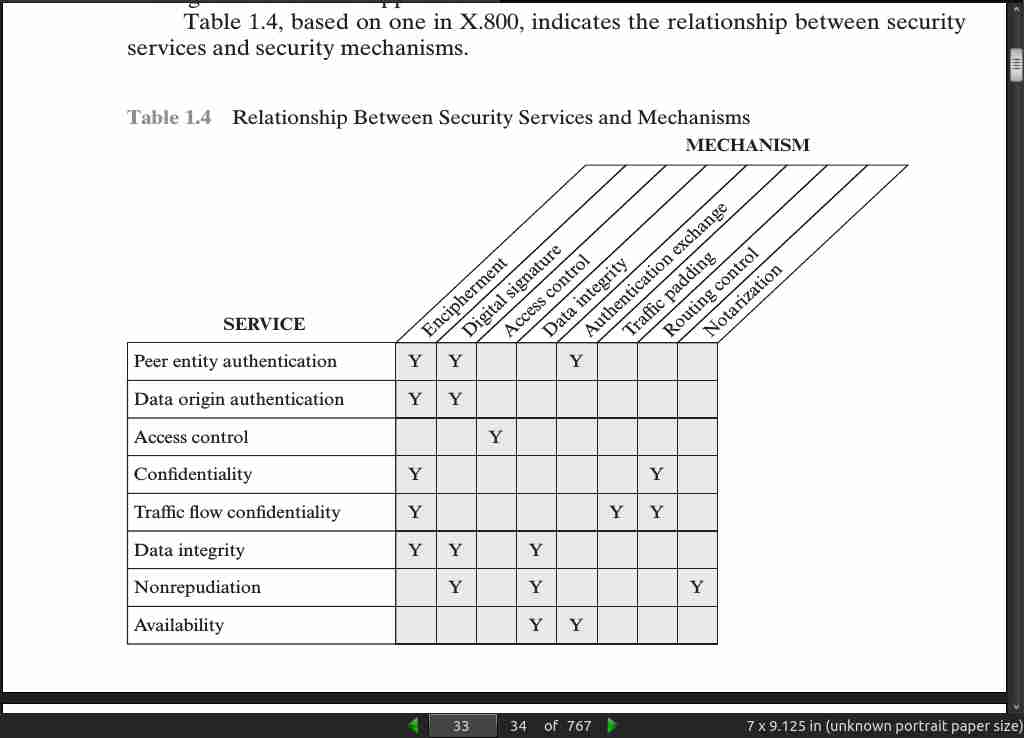
page 033:

page 039:

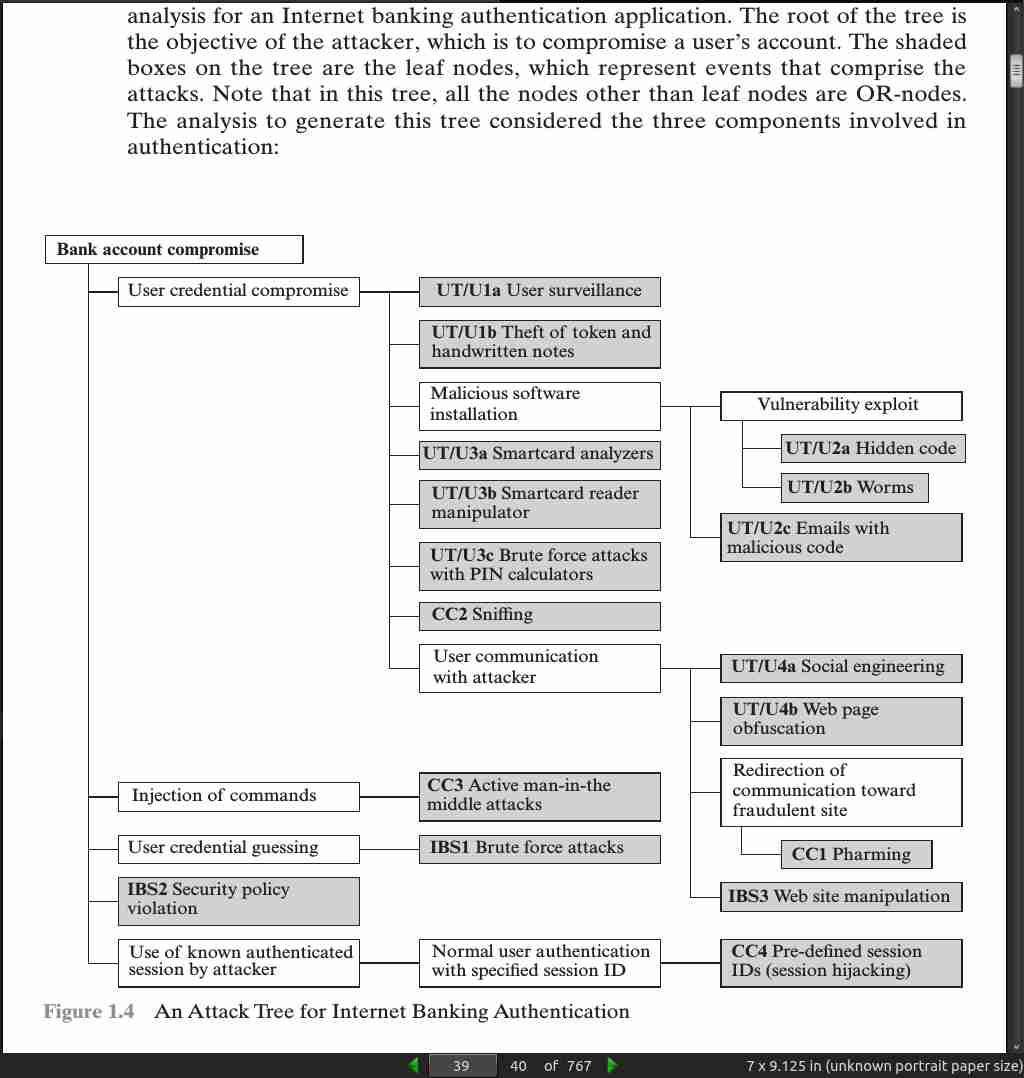
page 041:

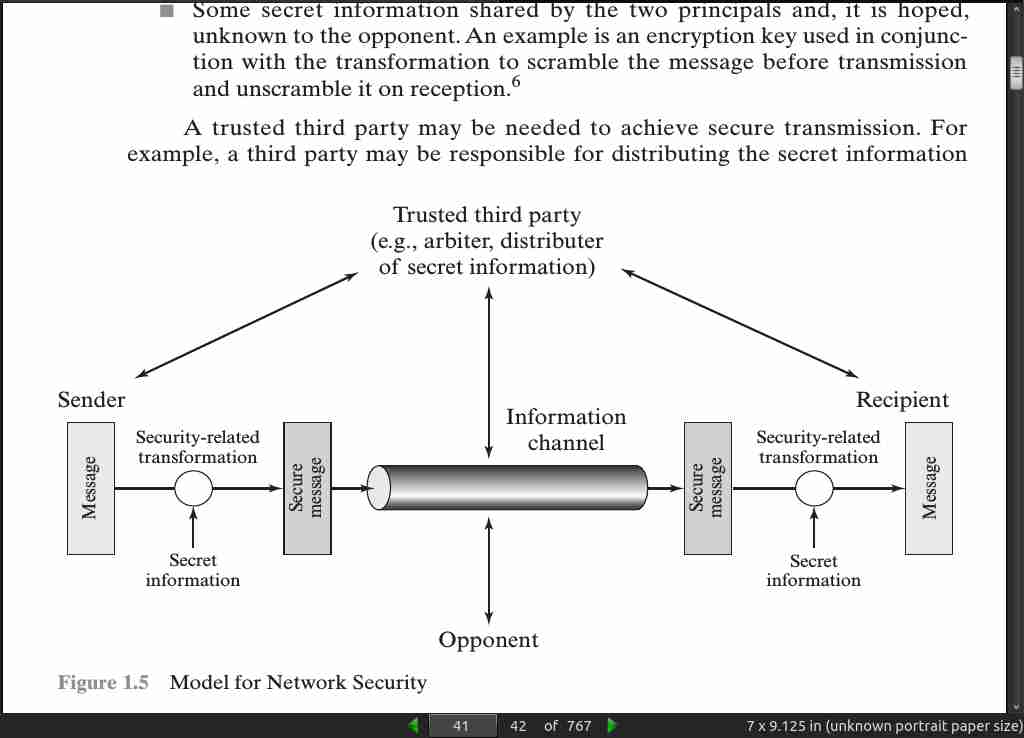
page 45:

• Read all of the classic papers cited in the Recommended Reading section for this chapter, available at the Author Web site at WilliamStallings.com/Cryptography. The papers are available at box.com/Crypto7e.

· 02: Introduction to Number Theory

page 48:

• a|b means a divides b

if a|1, then a = +-1
if a|b and b|a, then a = +-b
any b != 0 divides 0
if a|b and b|c, then a|c

If b|g and b|h, then b|(mg + nh) for arbitrary integers m and n.
To see this last point, note that
  If b|g, then g is of the form g = b * g1 for some integer g1.
  If b|h, then h is of the form h = b * h1 for some integer h1 .
So
  mg + nh = mbg1 + nbh1 = b * (mg1 + nh1)
and therefore b divides mg + nh.

• To calculate q and r with numpy:

np.floor(-11/7)
np.remainder(-11, 7)

page 49:

• Two integers are relatively prime if and only if their only common positive integer factor is 1.

page 50:

• gcd(a, b) = max[k, such that k|a and k|b]

• 8 and 15 are relatively prime because the positive divisors of 8 are 1, 2, 4, and 8, and the positive divisors of 15 are 1, 3, 5, and 15. So 1 is the only integer on both lists.

import numpy as np

def gcd(a, b):
  #q = np.floor(a/b)
  r = np.remainder(a, b)
  #print q, r
  if r > 0:
    return gcd(b, r)
  else:
    return b

def gcd_2(a, b):
  if b == 0:
    return a
  else:
    return gcd(b, np.remainder(a, b))

if __name__ == "__main__":
  print gcd(1160718174, 316258250)   #1078
  print gcd_2(1160718174, 316258250) #1078

page 050:

page 53:

>>> np.mod == np.remainder
True

• Two integers a and b are said to be congruent modulo n, if (a mod n) = (b mod n). This is written as a = b (mod n).

page 054:

page 55:

Define the set Z_n as the set of nonnegative integers less than n: Z n = {0, 1, …, (n - 1)}

page 056:

page 057:

page 58:

• In general, an integer has a multiplicative inverse in Z n if and only if that integer is relatively prime to n.

def mgcd(a, b):
  if b == 0:
    return a
  else:
    return mgcd(b, np.mod(a, b))

if __name__ == "__main__":
  print mgcd(1160718174, 316258250) #1078

page 059:

page 061:

page 064:

page 065:

page 067:

page 068:

page 069:

page 071:

page 076:

· 03: Classical Encryption Techniques

page 87:

• We assume that it is impractical to decrypt a message on the basis of the ciphertext plus knowledge of the encryption/decryption algorithm. In other words, we do not need to keep the algorithm secret; we need to keep only the key secret. This feature of symmetric encryption is what makes it feasible for widespread use. The fact that the algorithm need not be kept secret means that manufacturers can and have developed low-cost chip implementations of data encryption algorithms. These chips are widely available and incorporated into a number of products. With the use of symmetric encryption, the principal security problem is maintaining the secrecy of the key.

page 088:

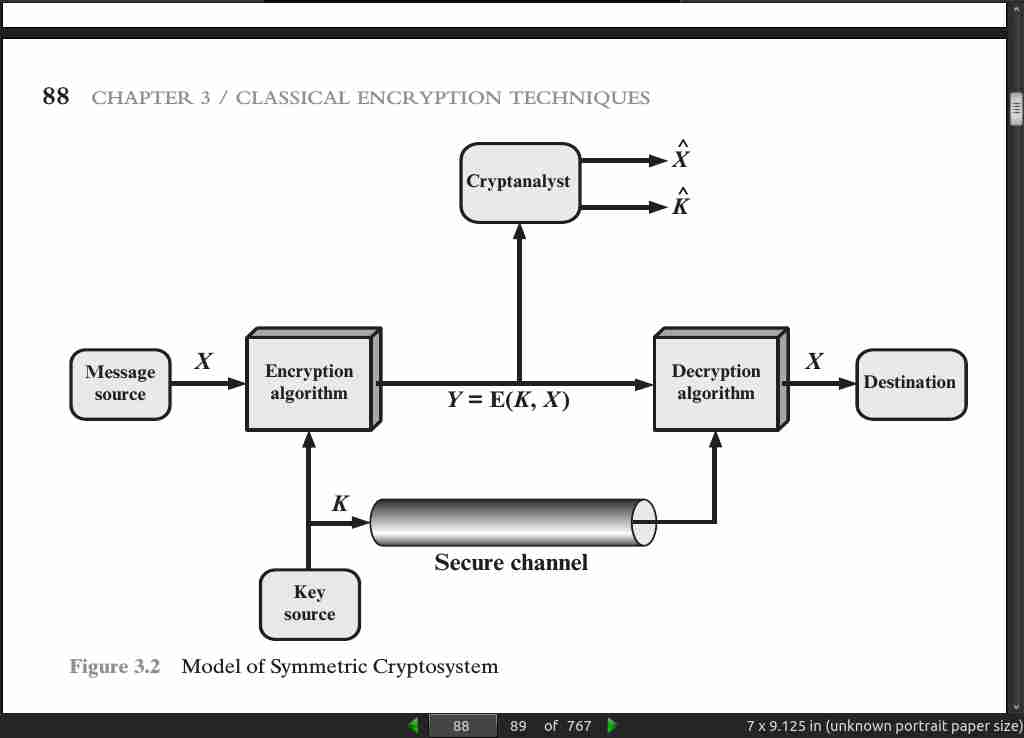
page 89:

• All encryption algorithms are based on two general principles: substitution, in which each element in the plaintext (bit, letter, group of bits or letters) is mapped into another element, and transposition, in which elements in the plaintext are rearranged.

• If both sender and receiver use the same key, the system is referred to as symmetric, single-key, secret-key, or conventional encryption. If the sender and receiver use different keys, the system is referred to as asymmetric, two-key, or public-key encryption.

page 91:

• With the exception of a scheme known as the one-time pad (described later in this chapter), there is no encryption algorithm that is unconditionally secure. Therefore, all that the users of an encryption algorithm can strive for is an algorithm that meets one or both of the following criteria:

• 1. The cost of breaking the cipher exceeds the value of the encrypted information.
• 2. The time required to break the cipher exceeds the useful lifetime of the information.

• An encryption scheme is said to be computationally secure if either of the foregoing two criteria are met.

page 095:

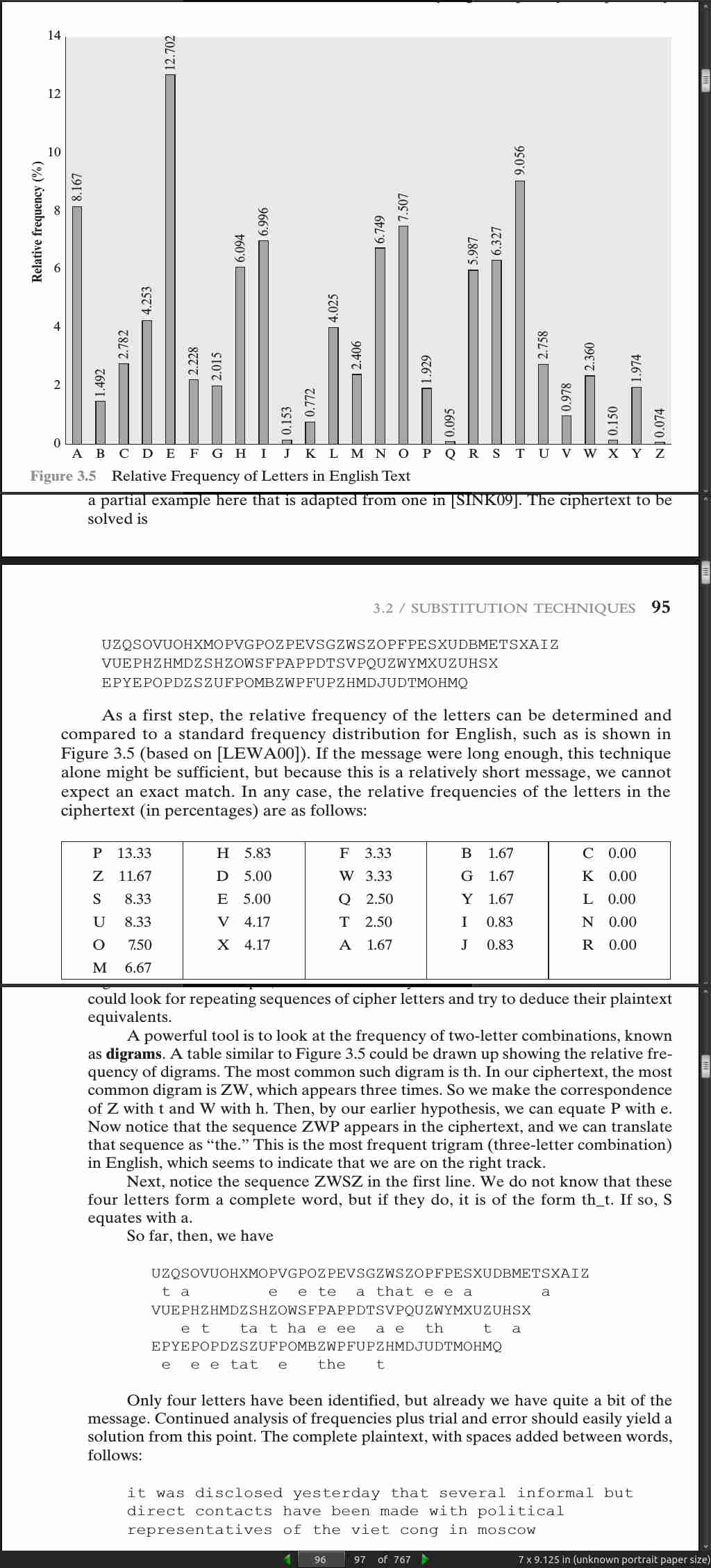
page 97:

• Playfair cipher

page 99:

• Hill cipher

page 104:

• Although the techniques for breaking a Vigenère cipher are by no means complex, a 1917 issue of Scientific American characterized this system as “impossible of translation.” This is a point worth remembering when similar claims are made for modern algorithms.

page 105:

• random key that is as long as the message, so that the key need not be repeated. In addition, the key is to be used to encrypt and decrypt a single message, and then is discarded. [one-time pad]

• a one-time pad, is unbreakable.

• Funny, saying this literally on the next page after warning against such claims.

page 111:

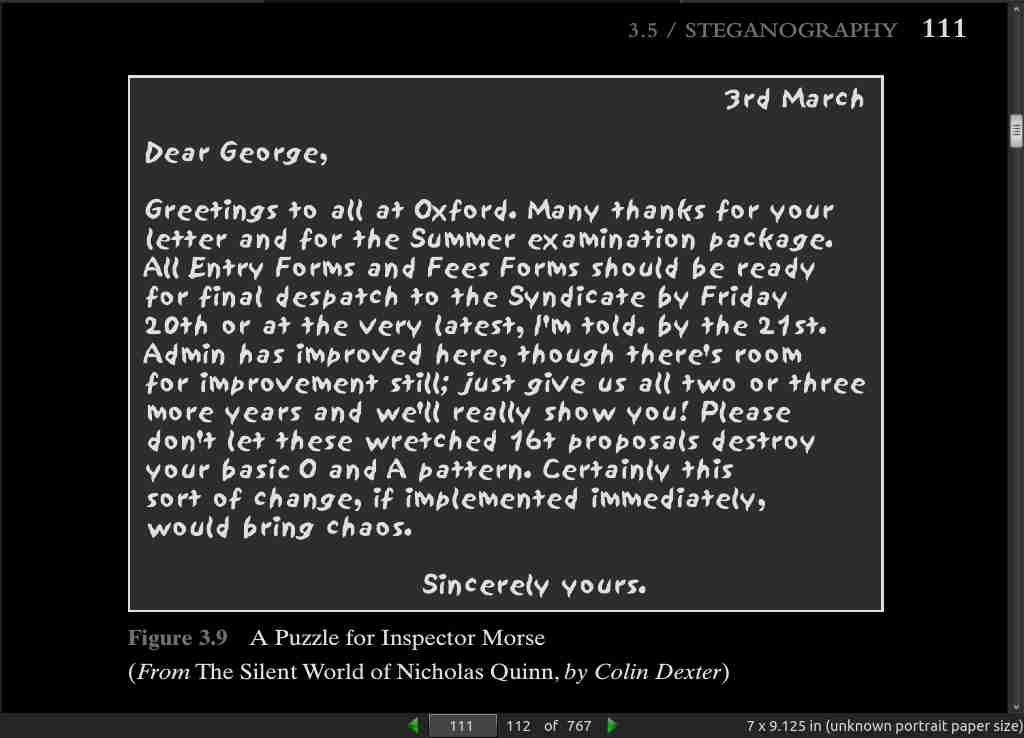
page 113:

page 117:

· 04: Block Ciphers and the Data Encryption Standard

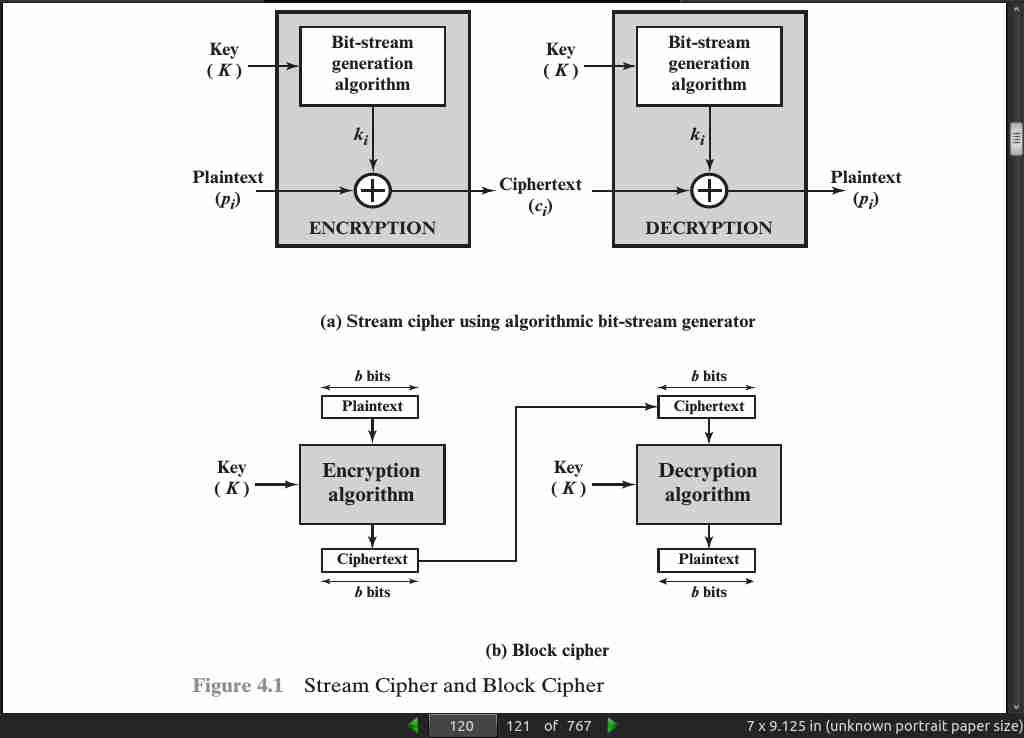
page 120:

page 124:

• diffusion, the sta- tistical structure of the plaintext is dissipated into long-range statistics of the ciphertext. This is achieved by having each plaintext digit affect the value of many ciphertext digits; generally, this is equivalent to having each ciphertext digit be affected by many plaintext digits.

page 125:

• confusion seeks to make the relationship between the statistics of the ciphertext and the value of the encryption key as complex as possible, again to thwart attempts to discover the key.

page 126:

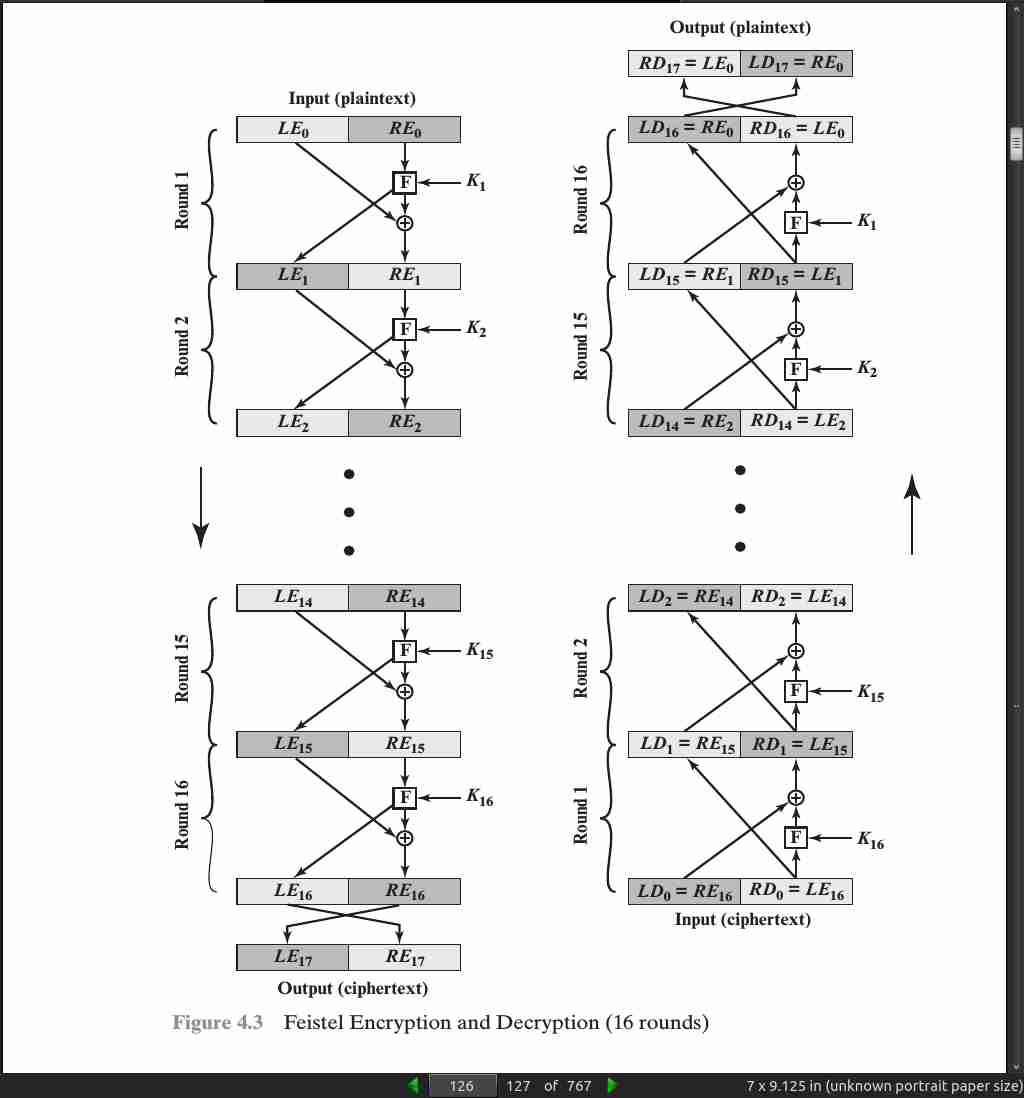
page 127:

• Block size: Larger block sizes mean greater security (all other things being equal) but reduced encryption/decryption speed for a given algorithm. The greater security is achieved by greater diffusion. Traditionally, a block size of 64 bits has been considered a reasonable tradeoff and was nearly universal in block cipher design. However, the new AES uses a 128-bit block size.

• Key size: Larger key size means greater security but may decrease encryption/ decryption speed. The greater security is achieved by greater resistance to brute-force attacks and greater confusion. Key sizes of 64 bits or less are now widely considered to be inadequate, and 128 bits has become a common size.

• Number of rounds: The essence of the Feistel cipher is that a single round offers inadequate security but that multiple rounds offer increasing security. A typical size is 16 rounds.

• Subkey generation algorithm: Greater complexity in this algorithm should lead to greater difficulty of cryptanalysis.

• Round function F: Again, greater complexity generally means greater resistance to cryptanalysis.

page 128:

page 130:

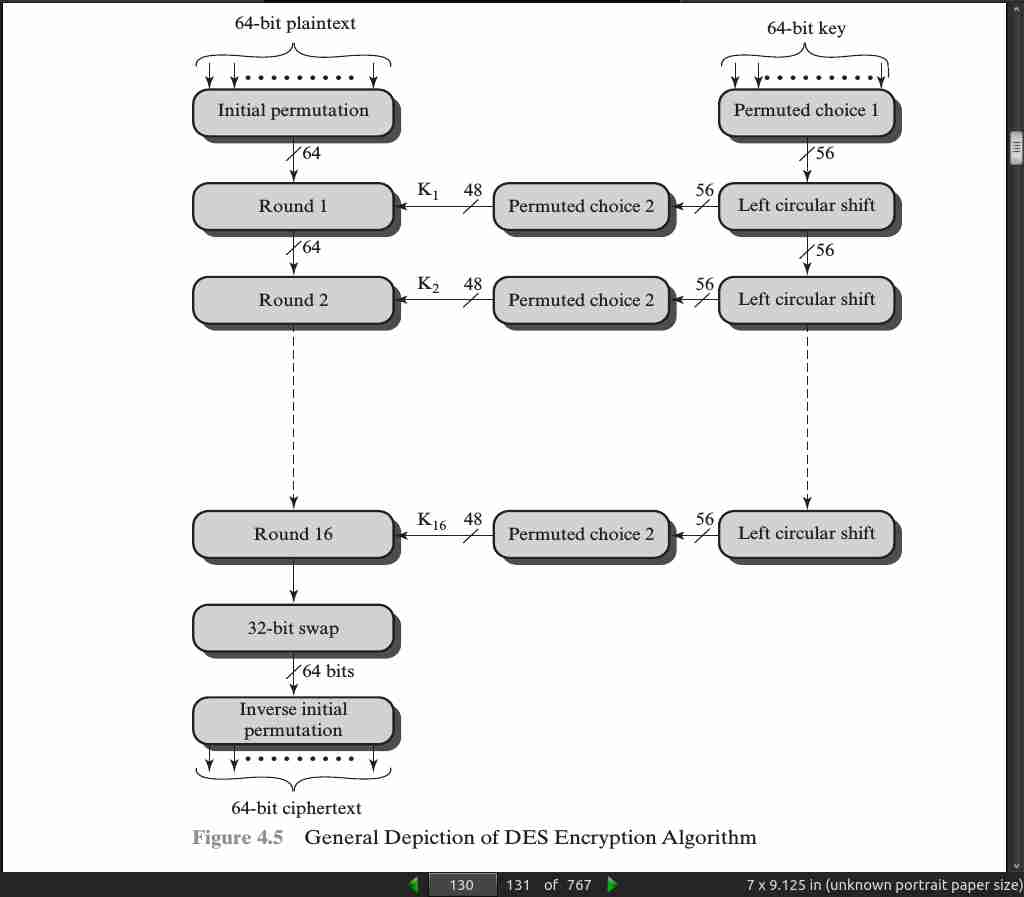
page 132:

• Avalanche effect = a small change in the plaintext produces a significant change in the ciphertext.

· 05: Finite Fields

page 143:

• A group G, sometimes denoted by {G, # }, is a set of elements with a binary operation denoted by # that associates to each ordered pair (a, b) of elements in G an element (a # b) in G, such that the following axioms are obeyed:

(A1) Closure: If a and b belong to G, then a # b is also in G.

(A2) Associative: a # (b # c) = (a # b) # c for all a, b, c in G.

(A3) Identity element: There is an element e in G such that a # e = e # a = a
for all a in G.

(A4) Inverse element: For each a in G, there is an element a′ in G such that a
# a′ = a′ # a = e.

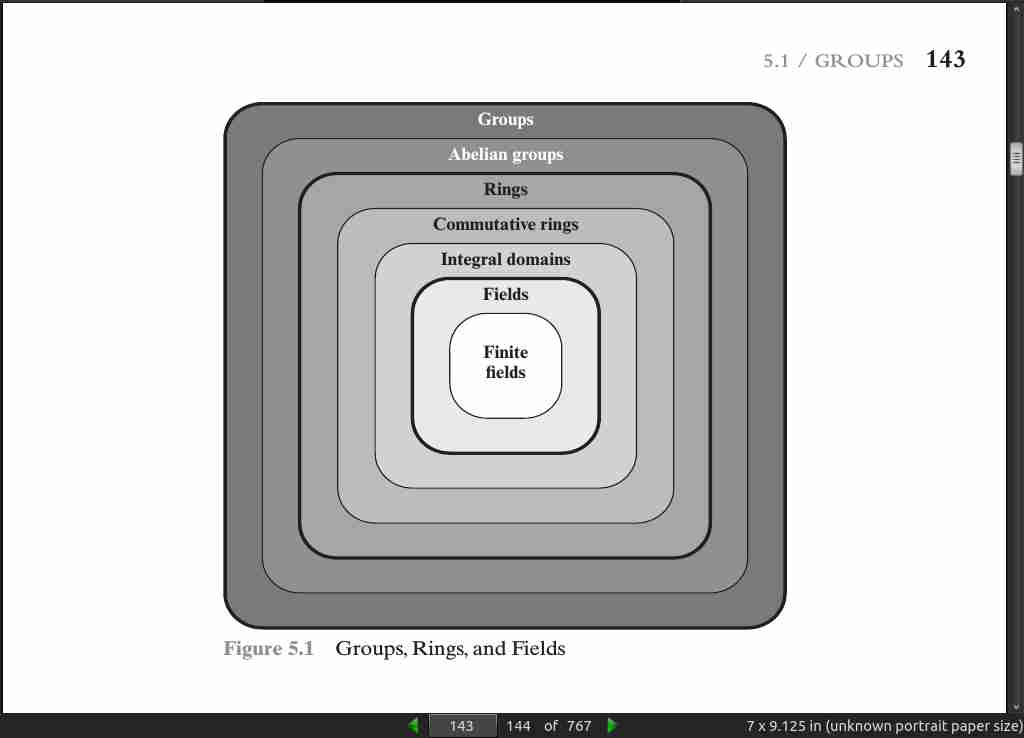
page 145:

• In essence, a ring is a set of elements in which we can do addition, subtraction [a - b = a + ( -b)], and multiplication without leaving the set.

• With respect to addition and multiplication, the set of all n-square matrices over the real numbers is a ring.

page 146:

• In essence, a field is a set of elements in which we can do addition, subtraction, multiplication, and division without leaving the set. Division is defined with the fol- lowing rule: a/b = a(b^-1).

page 147:

• the order of a finite field (number of elements in the field) must be a power of a prime p^n, where n is a positive integer. The finite field of order p^n is generally written GF(p^n); GF stands for Galois field, in honor of the mathematician who first studied finite fields.

page 148:

page 151:

page 152:

page 153:

page 154:

• in GF(2), addition is equivalent to the XOR operation, and multiplication is equivalent to the logical AND operation. Further, addition and subtraction are equivalent mod 2:

1 + 1 = 1 - 1 = 0
1 + 0 = 1 - 0 = 1
0 + 1 = 0 - 1 = 1

page 156:

• gcd[a(x), b(x)] = gcd[b(x), a(x) mod b(x)]

page 160:

page 164:

• addition of two polynomials in GF(2^n) corresponds to a bitwise XOR operation.

page 165:

• In general, in GF(2^n) with an nth-degree polynomial p(x), we have x^n mod p(x) = [p(x) - x^n].

· 06: Advanced Encryption Standard

page 178:

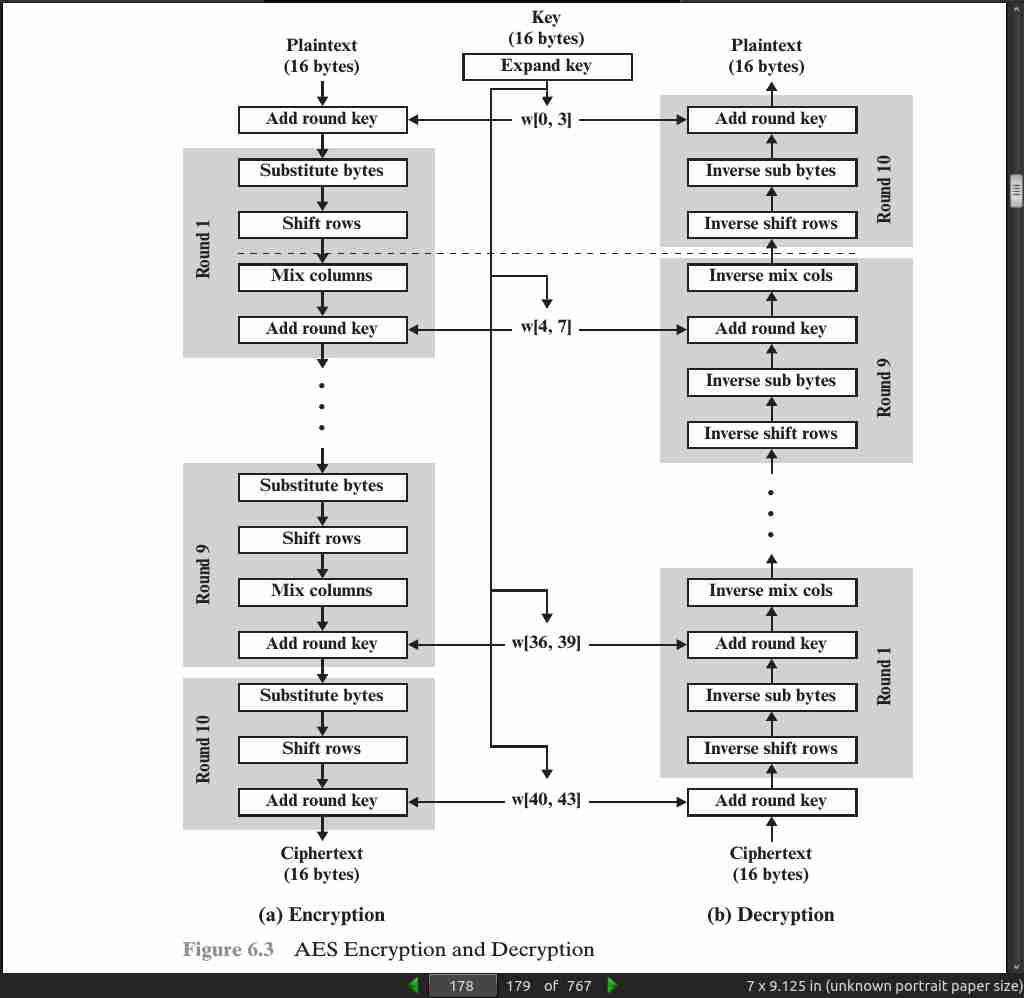
page 179:

page 185:

page 186:

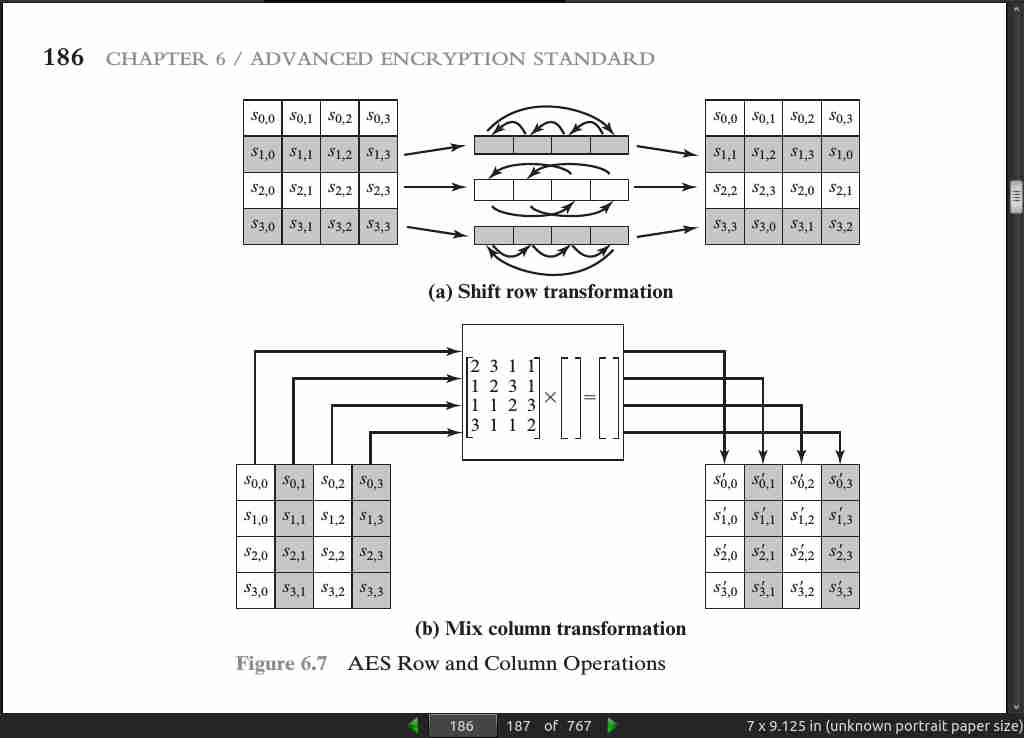
page 187:

page 189:

page 190:

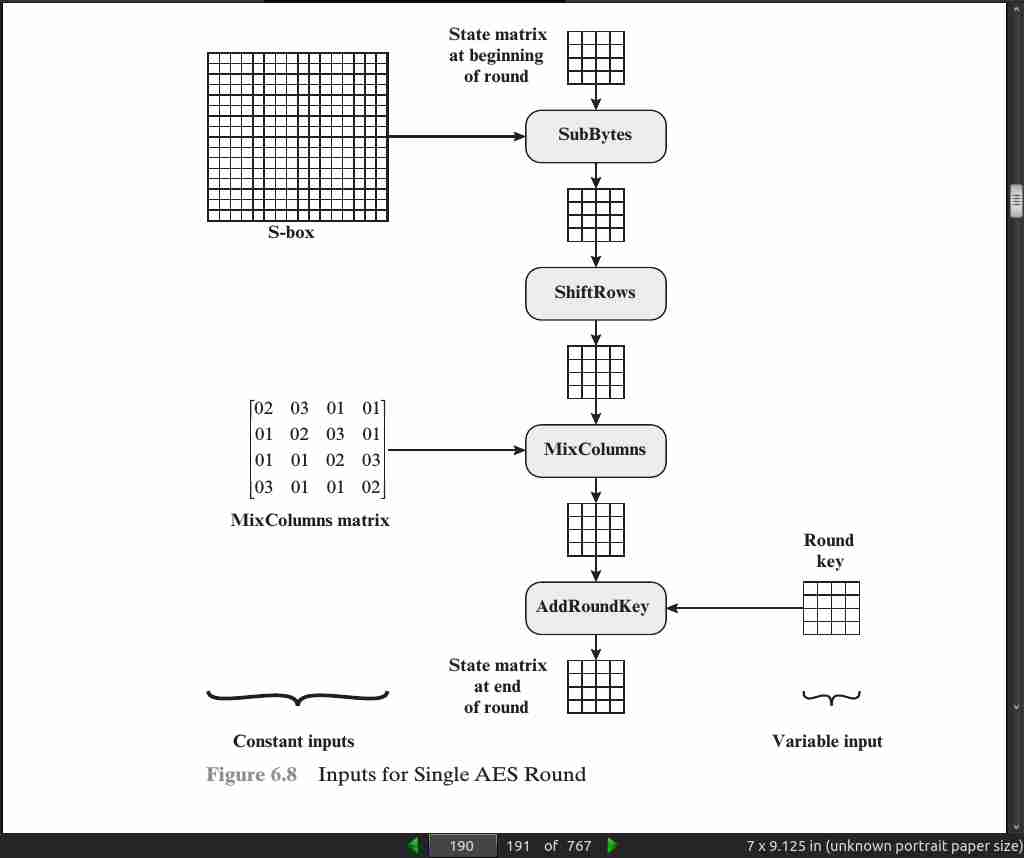
page 197:

• the AES decryption cipher is not identical to the encryption cipher (Figure 6.3). That is, the sequence of transformations for decryption differs from that for encryption, although the form of the key schedules for encryption and decryption is the same. This has the disadvantage that two separate software or firmware modules are needed for applications that require both encryption and decryption. There is, however, an equivalent version of the decryption algorithm that has the same structure as the encryption algorithm. The equivalent version has the same sequence of transformations as the encryption algorithm (with transformations replaced by their inverses). To achieve this equivalence, a change in key schedule is needed.

page 198:

• an encryption round has the structure SubBytes, ShiftRows, MixColumns, AddRoundKey. The standard decryption round has the structure InvShiftRows, InvSubBytes, AddRoundKey, InvMixColumns. Thus, the first two stages of the decryption round need to be interchanged, and the second two stages of the decryption round need to be interchanged.

• InvShiftRows[InvSubBytes(Si)] = InvSubBytes[InvShiftRows(S_i)]

• InvMixColumns(Si ^ w_j) = [InvMixColumns(S_i)] ^ [InvMixColumns(wj)]

page 199:

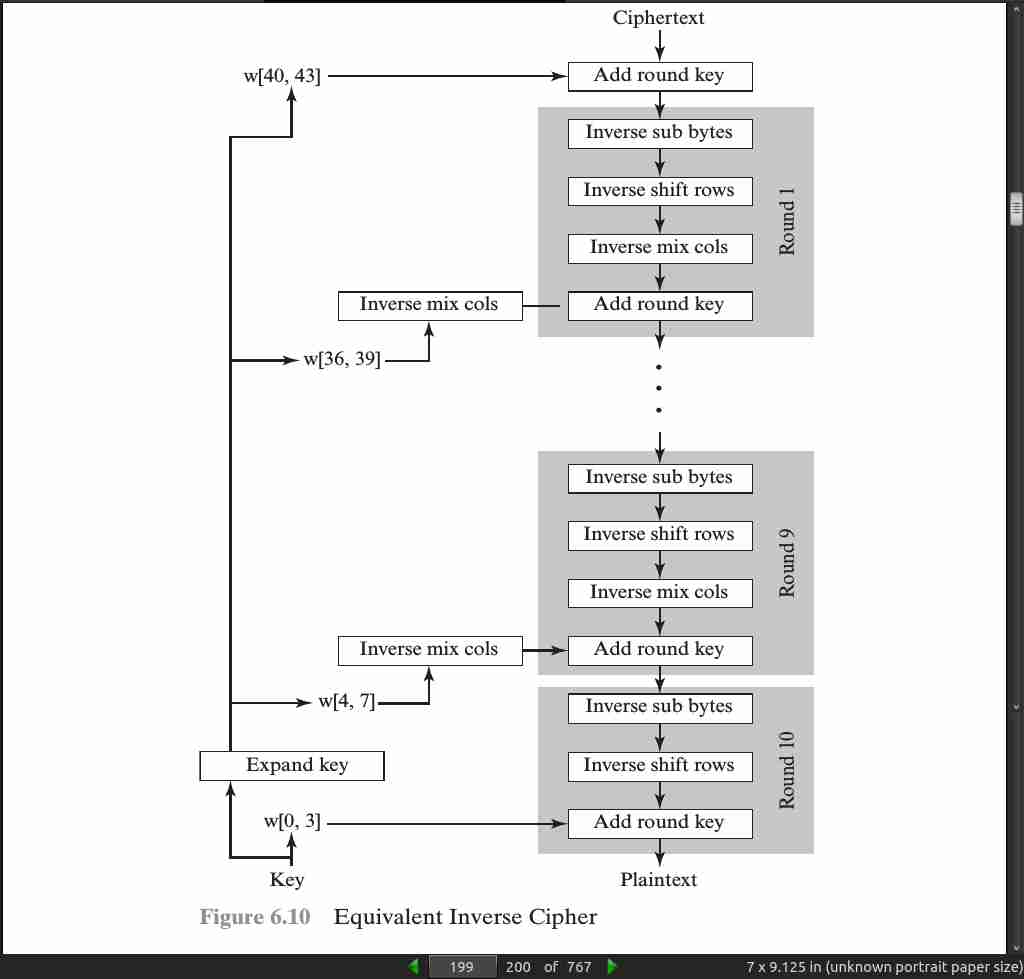
· 07: Block Cipher Operation

page 214:

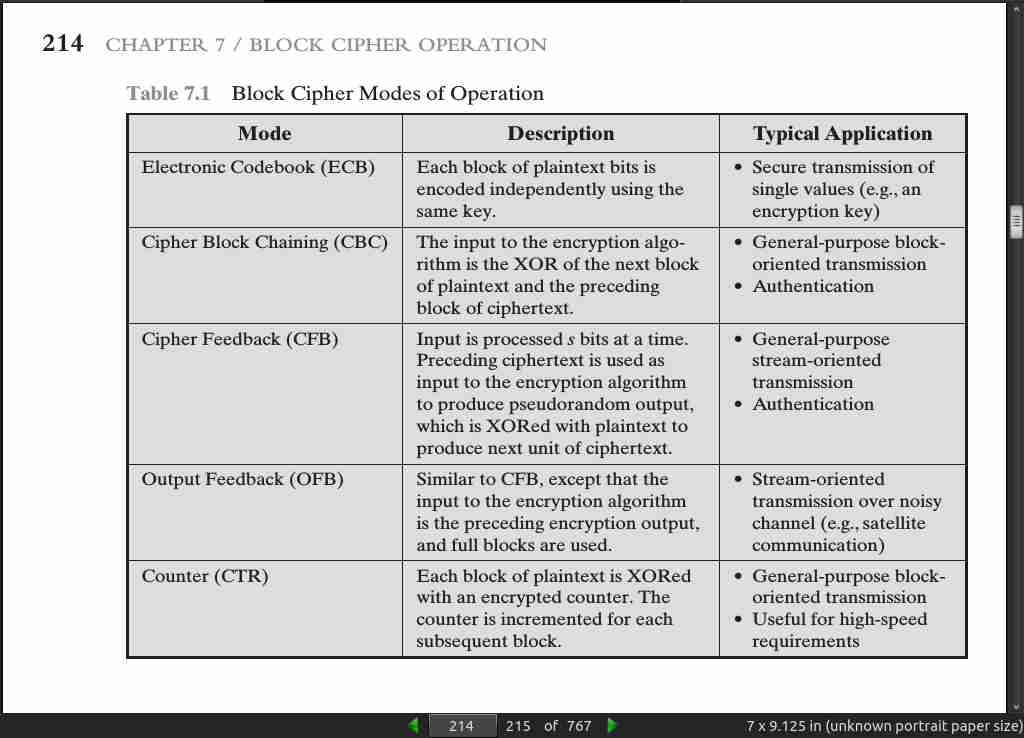
page 215:

• For lengthy messages, the ECB (electronic code book) mode may not be secure. If the message is highly structured, it may be possible for a cryptanalyst to exploit these regularities.

page 216:

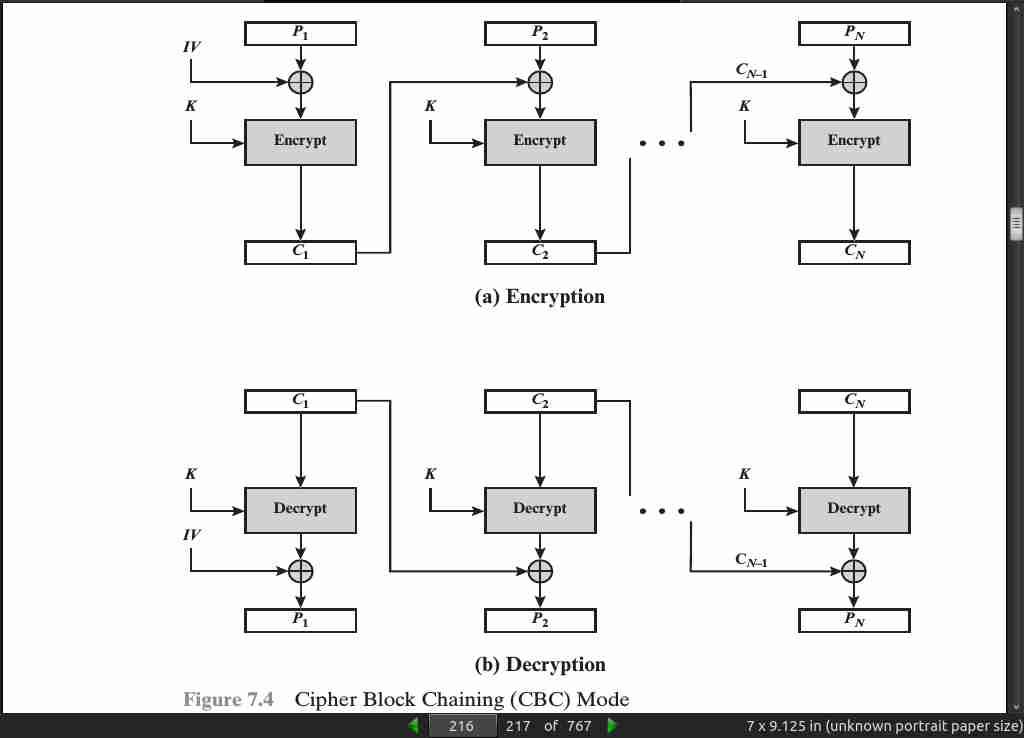
page 218:

• In conclusion, because of the chaining mechanism of CBC (cipher block chaining), it is an appropriate mode for encrypting messages of length greater than b bits.

• In addition to its use to achieve confidentiality, the CBC mode can be used for authentication. This use is described in Chapter 12.

• For AES, DES, or any block cipher, encryption is performed on a block of b bits. In the case of DES, b = 64 and in the case of AES, b = 128. However, it is possible to convert a block cipher into a stream cipher, using one of the three modes to be discussed in this and the next two sections: cipher feedback (CFB) mode, output feedback (OFB) mode, and counter (CTR) mode. A stream cipher eliminates the need to pad a message to be an integral number of blocks. It also can operate in real time.

page 219:

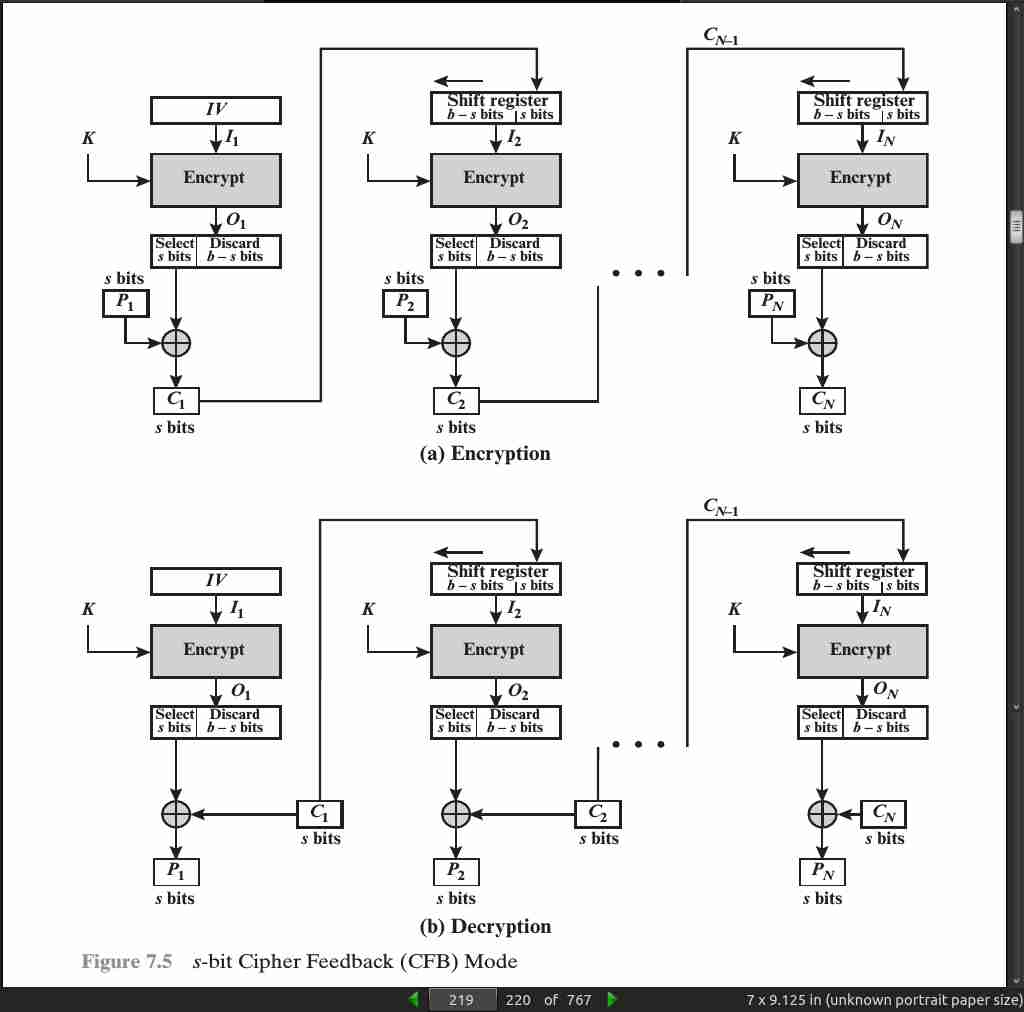
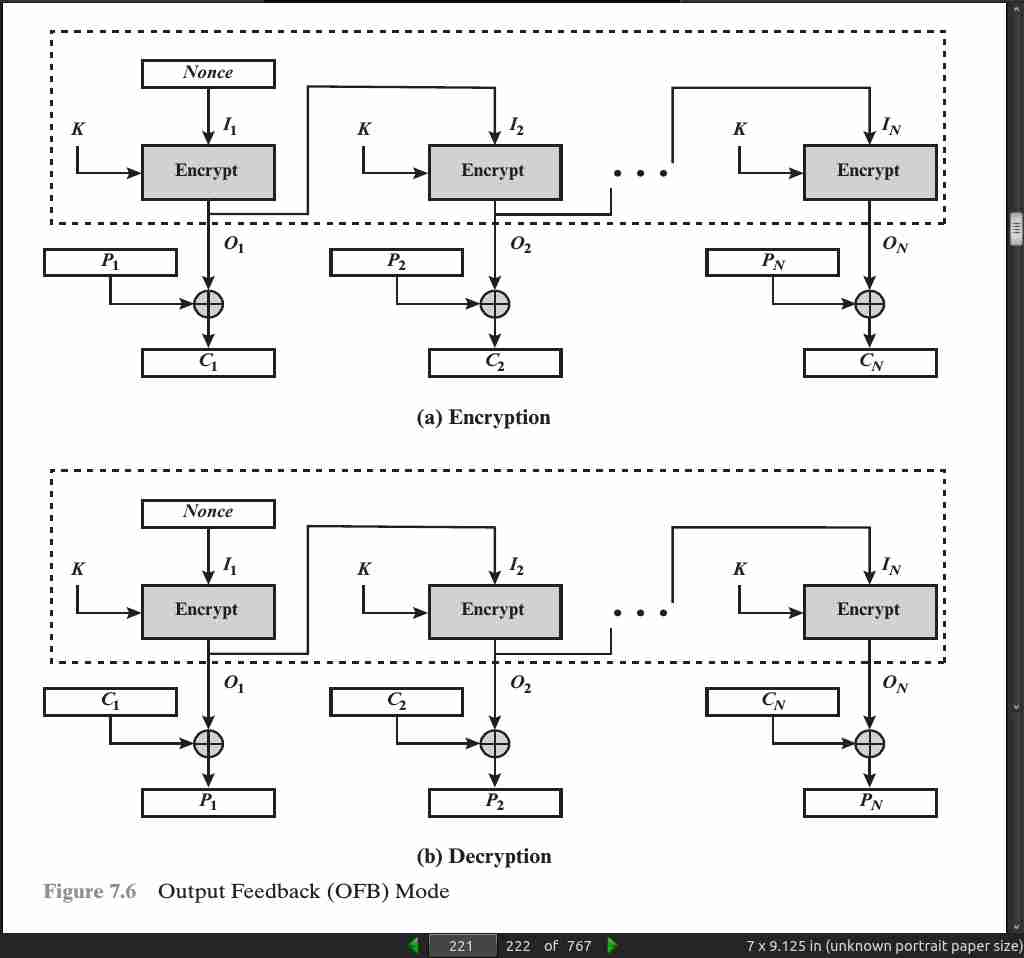
page 221:

• One advantage of the OFB (output feedback) method is that bit errors in transmission do not propagate. For example, if a bit error occurs in C1, only the recovered value of P1 is affected

• The disadvantage of OFB is that it is more vulnerable to a message stream modification attack than is CFB. Consider that complementing a bit in the ciphertext complements the corresponding bit in the recovered plaintext. Thus, controlled changes to the recovered plaintext can be made. This may make it possible for an opponent, by making the necessary changes to the checksum portion of the message as well as to the data portion, to alter the ciphertext in such a way that it is not detected by an error-correcting code.

• One distinction from the stream ciphers we discuss in Chapter 8 is that OFB encrypts plaintext a full block at a time, where typically a block is 64 or 128 bits. Many stream ciphers encrypt one byte at a time.

page 223:

• Hardware efficiency: Unlike the three chaining modes, encryption (or decryption) in CTR (counter) mode can be done in parallel on multiple blocks of plaintext or ciphertext. For the chaining modes, the algorithm must complete the computation on one block before beginning on the next block.

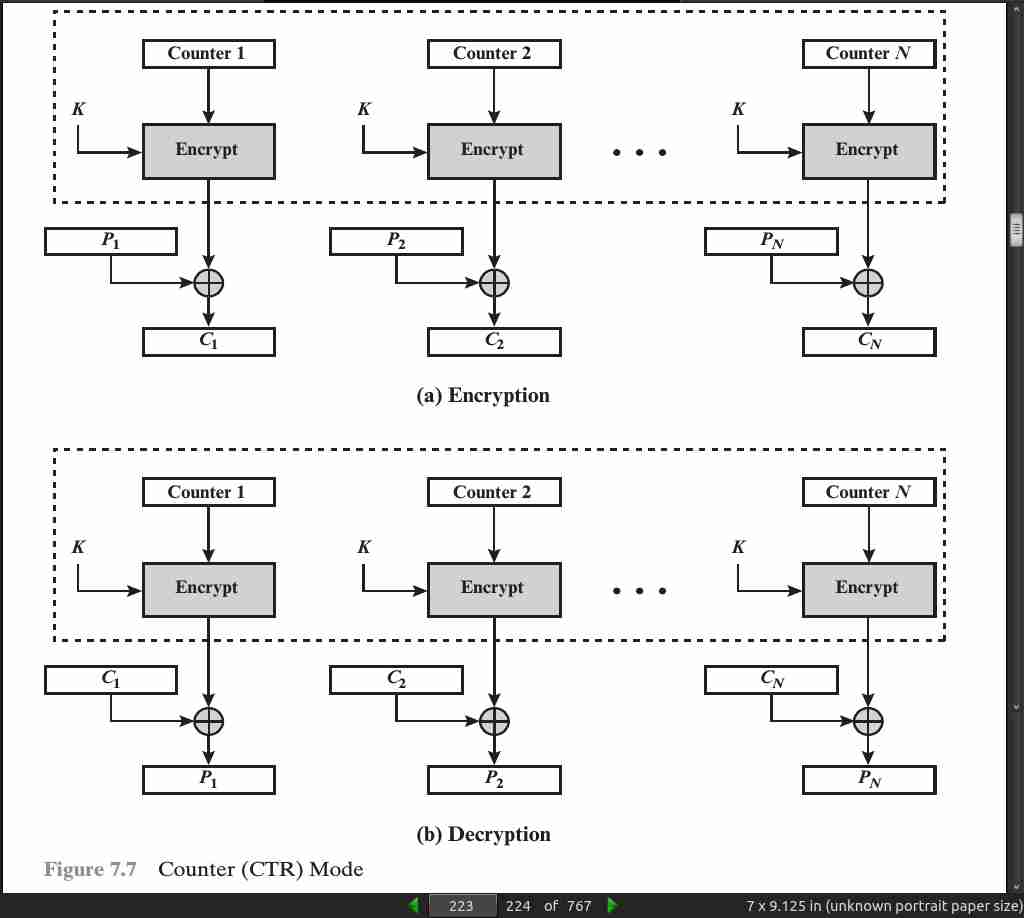
page 224:

• Preprocessing: The execution of the underlying encryption algorithm does not depend on input of the plaintext or ciphertext. Therefore, if sufficient memory is available and security is maintained, preprocessing can be used to prepare the output of the encryption boxes that feed into the XOR functions, as in Figure 7.7. When the plaintext or ciphertext input is presented, then the only computation is a series of XORs. Such a strategy greatly enhances throughput.

• Provable security: It can be shown that CTR is at least as secure as the other modes discussed in this chapter.

page 225:

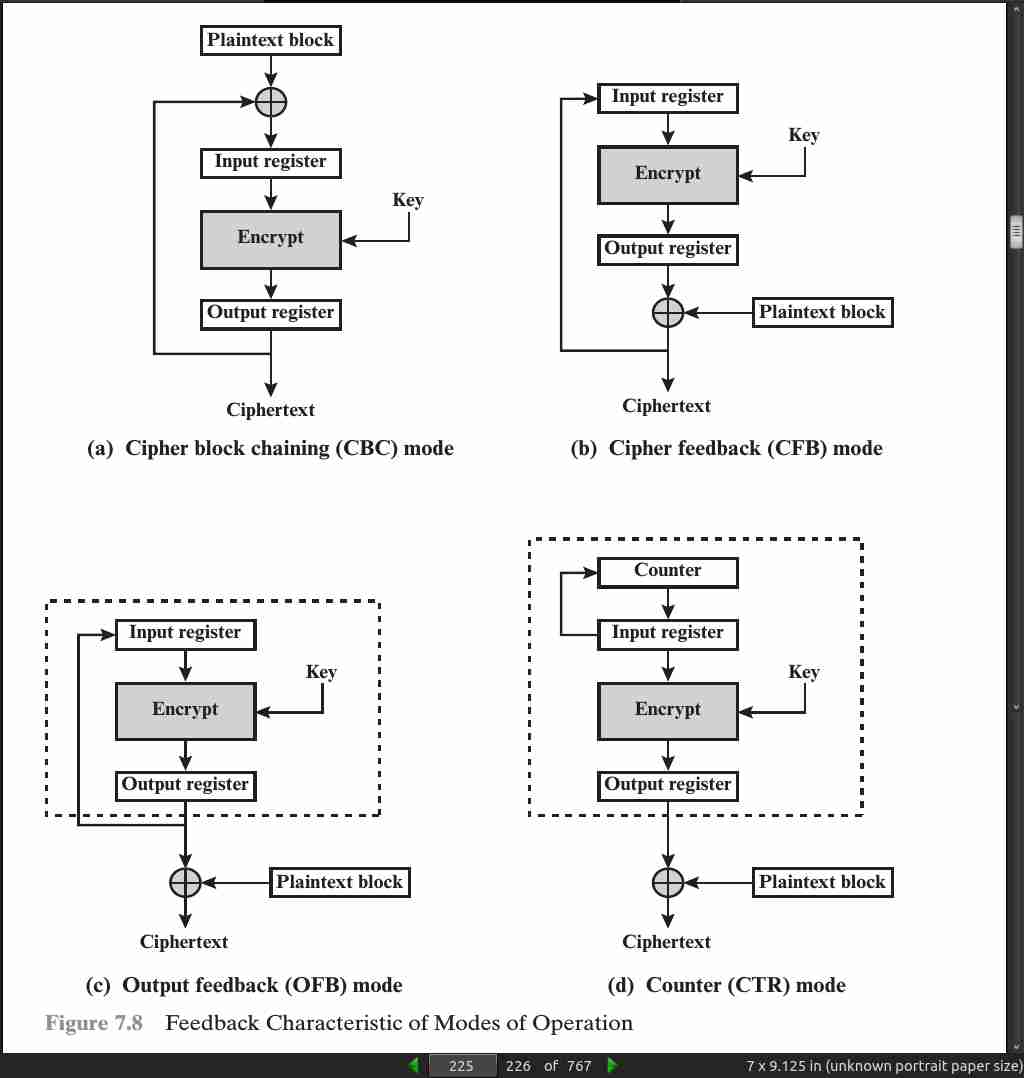
page 231:

• Format-preserving encryption (FPE) refers to any encryption technique that takes a plaintext in a given format and produces a ciphertext in the same format. For example, credit cards consist of 16 decimal digits.

• FPE facilitates the retrofitting of encryption technology to legacy applications, where a conventional encryption mode might not be feasible because it would disrupt data fields/pathways.

· 08: Random Bit Generation and Stream Ciphers

page 254:

page 259:

• Thus, the generating function becomes

m     the modulus                   m > 0
a     the multiplier                0 < a < m
c     the increment                 0 <= c < m
X_0   the starting value, or seed   0 <= X_0 < m

X_n + 1 = (aX_n) mod (2^31 - 1)

• Of the more than 2 billion possible choices for a, only a handful of multipliers pass all three tests. One such value is a = 75 = 16807, which was originally selected for use in the IBM 360 family of computers [LEWI69]. This generator is widely used and has been subjected to a more thorough testing than any other PRNG [pseudo random number generator]. It is frequently recommended for statistical and simulation work (e.g., [JAIN91]).

page 260:

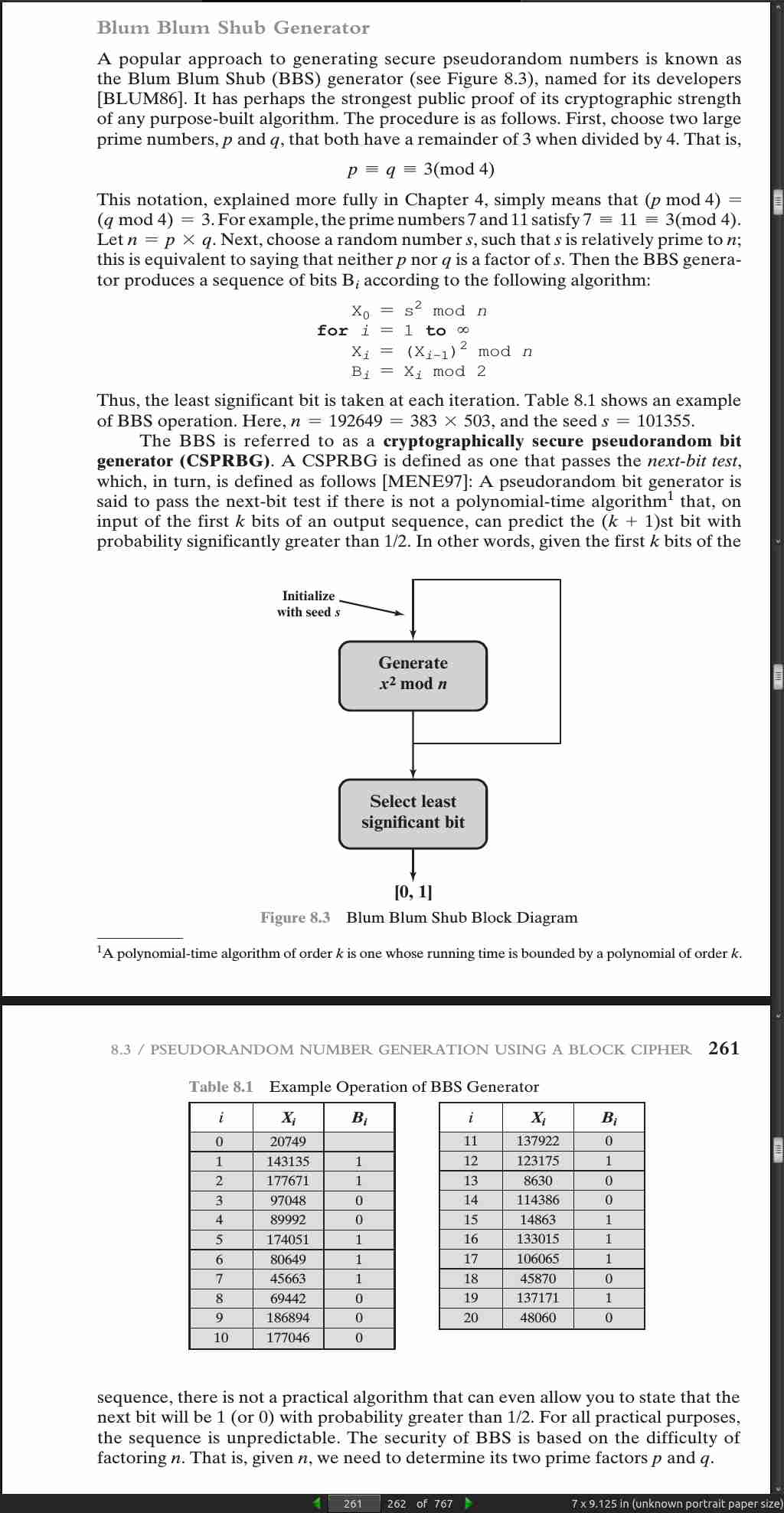
page 262:

• A random bit sequence of 256 bits was obtained from random.org, which uses three radios tuned between stations to pick up atmospheric noise.

· 09: Principles of Public-Key Cryptosystems

page 286:

• 1 Diffie and Hellman first publicly introduced the concepts of public-key cryptography in 1976. Hellman credits Merkle with independently discovering the concept at that same time, although Merkle did not publish until 1978 [MERK78]. In fact, the first unclassified document describing public-key distribution and public-key cryptography was a 1974 project proposal by Merkle (http://merkle.com/1974). However, this is not the true beginning. Admiral Bobby Inman, while director of the National Security Agency (NSA), claimed that public-key cryptography had been discovered at NSA in the mid-1960s [SIMM93]. The first documented introduction of these concepts came in 1970, from the Communications-Electronics Security Group, Britain’s counterpart to NSA, in a classified report by James Ellis [ELLI70]. Ellis referred to the technique as non-secret encryption and describes the discovery in [ELLI99].

page 290:

• You can encrypt the whole message for confidentiality, but this means you need to keep the cipher and plain texts to authenticate. You can encrypt only a small block of the message to authenticate, but with no confidentiality.

page 291:

• to provide both the authentication function and confidentiality by a double use of the public-key scheme (Figure 9.4):

Z = E(PU_b, E(PR_a,X))
X = D(PU_a, D(PR_b,Z))

page 294:

• Another form of attack is to find some way to compute the private key given the public key. To date, it has not been mathematically proven that this form of attack is infeasible for a particular public-key algorithm. Thus, any given algorithm, including the widely used RSA algorithm, is suspect. The history of cryptanalysis shows that a problem that seems insoluble from one perspective can be found to have a solution if looked at in an entirely different way.

• Finally, there is a form of attack that is peculiar to public-key systems. This is, in essence, a probable-message attack. Suppose, for example, that a message were to be sent that consisted solely of a 56-bit DES key. An adversary could encrypt all possible 56-bit DES keys using the public key and could discover the encrypted key by matching the transmitted ciphertext. Thus, no matter how large the key size of the public-key scheme, the attack is reduced to a brute-force attack on a 56-bit key. This attack can be thwarted by appending some random bits to such simple messages.

page 295:

• We are now ready to state the RSA scheme. The ingredients are the following:

p, q, two prime numbers                  (private, chosen)
n = pq                                   (public, calculated)
e, with gcd(f(n), e) = 1; 1 6 e 6 f(n)   (public, chosen)
d K e -1 (mod f(n))                      (private, calculated)

page 296:

• For this example, the keys were generated as follows.

1. Select two prime numbers, p = 17 and q = 11.
2. Calculate n = pq = 17 * 11 = 187.
3. Calculate f(n) = (p - 1)(q - 1) = 16 * 10 = 160.
4. Select e such that e is relatively prime to f(n) = 160 and less than f(n); 
we choose e = 7.
5. Determine d such that de K 1 (mod 160) and d 6 160. The correct value is
d = 23, because 23 * 7 = 161 = (1 * 160) + 1; d can be calculated using
the extended Euclid’s algorithm (Chapter 2).

• The resulting keys are public key PU = {7, 187} and private key PR = {23, 187}.

• The example shows the use of these keys for a plaintext input of M = 88. For encryption, we need to calculate C = 887 mod 187. Exploiting the properties of modular arithmetic, we can do this as follows.

88^7 mod 187 = [(88^4 mod 187) * (88^2 mod 187) * (88^1 mod 187)] mod 187
88^1 mod 187 = 88
88^2 mod 187 = 7744 mod 187 = 77
88^4 mod 187 = 59,969,536 mod 187 = 132
88^7 mod 187 = (88 * 77 * 132) mod 187 = 894,432 mod 187 = 11

• For decryption, we calculate M = 11 23 mod 187:

11^23 mod 187 = [(11^1 mod 187) * (11^2 mod 187) * (11^4 mod 187) 
                * (11^8 mod 187) * (11^8 mod 187)] mod 187
11^1 mod 187 = 11
11^2 mod 187 = 121
11^4 mod 187 = 14,641 mod 187 = 55
11^8 mod 187 = 214,358,881 mod 187 = 33
11^23 mod 187 = (11 * 121 * 55 * 33 * 33) mod 187 = 79,720,245 mod 187 = 88

page 297:

page 298:

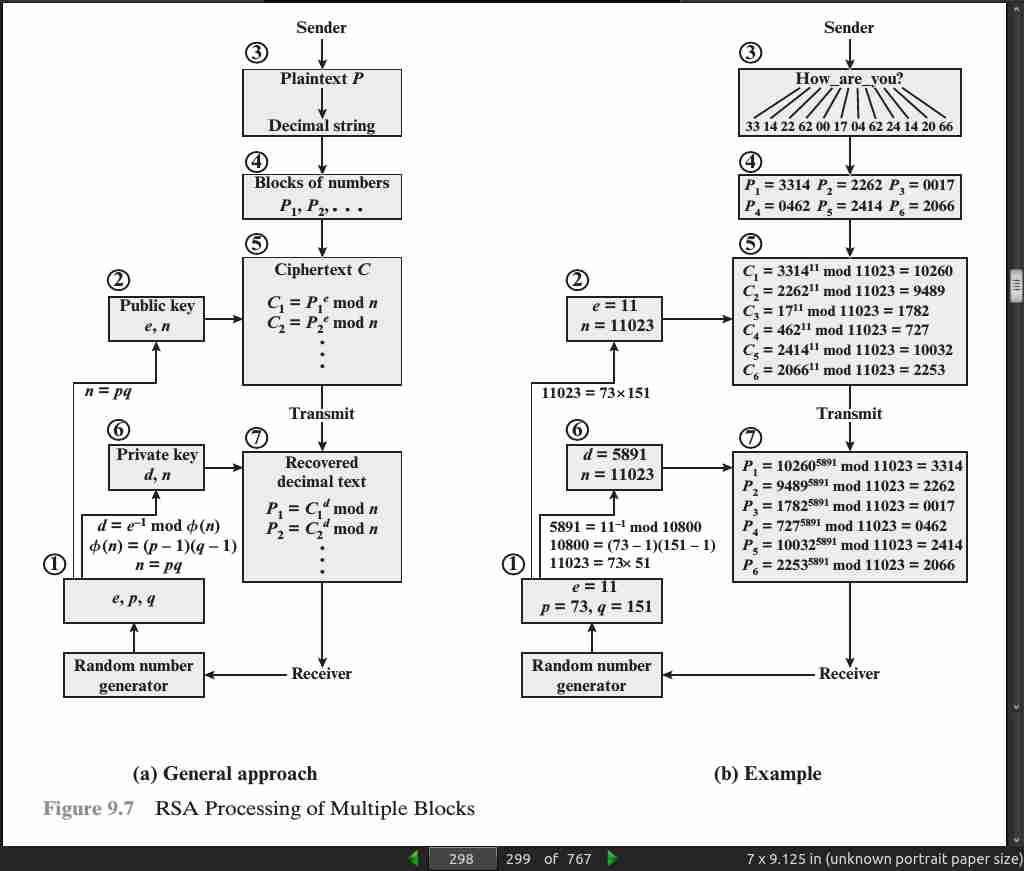
page 299:

• To speed up the operation of the RSA algorithm using the public key, a specific choice of e is usually made. The most common choice is 65537 (216 + 1); two other popular choices are 3 and 17. Each of these choices has only two 1 bits, so the number of multiplications required to per- form exponentiation is minimized.

page 303:

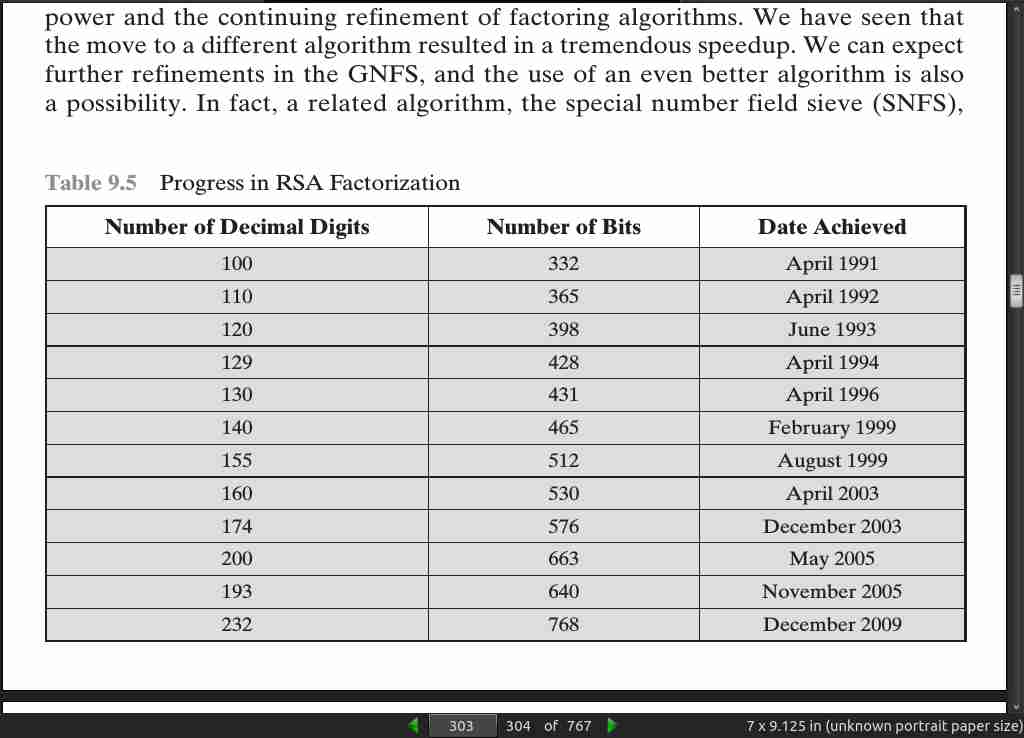
· 10: Other Public-Key Cryptosystems

page 315:

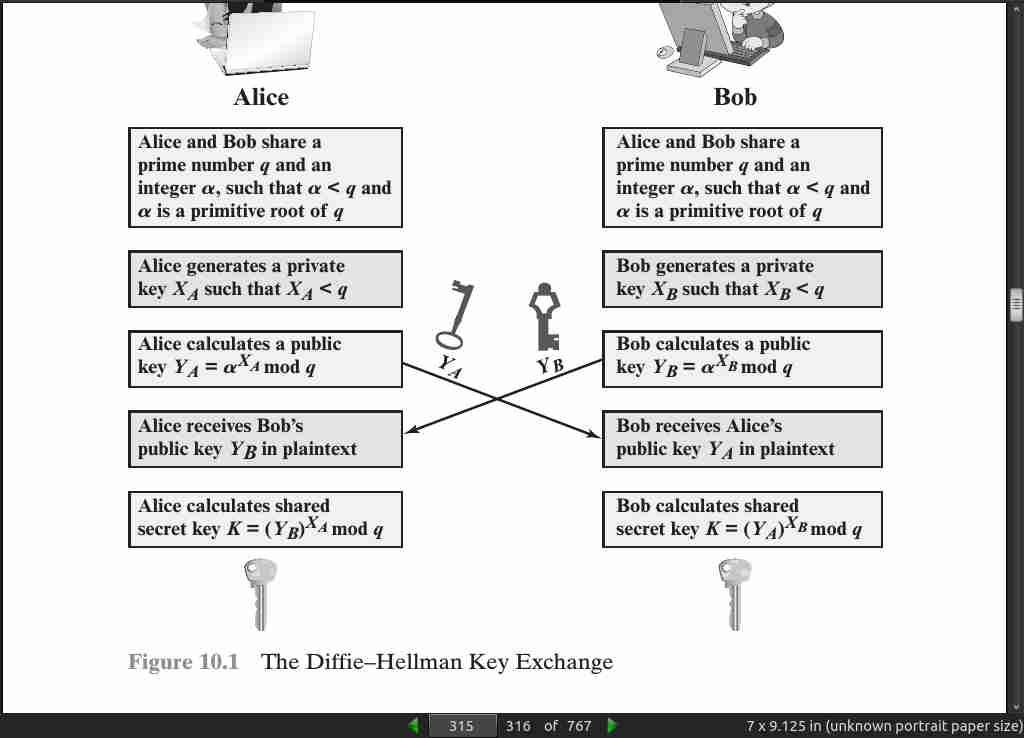
page 316:

page 320:

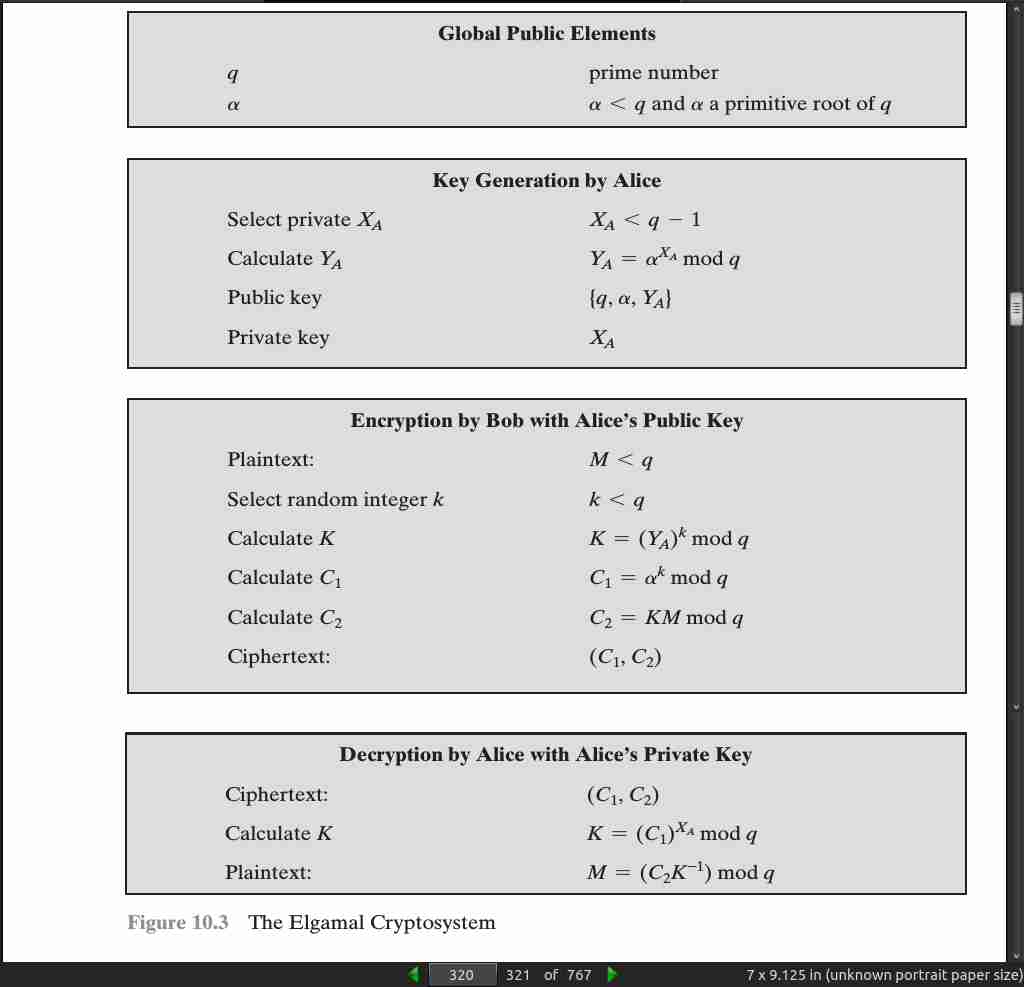
page 321:

page 323:

• Elliptic curves are not ellipses. They are so named because they are described by cubic equations, similar to those used for calculating the circumference of an ellipse. In general, cubic equations for elliptic curves take the following form, known as a Weierstrass equation:

y^2 + axy + by = x^3 + cx^2 + dx + e

• In geometric terms, the rules for addition can be stated as follows: If three points on an elliptic curve lie on a straight line, their sum is O.

page 324:

• 1. O serves as the additive identity. Thus O = -O; for any point P on the elliptic curve, P + O = P. In what follows, we assume P != O and Q != O.
• 2. The negative of a point P is the point with the same x coordinate but the negative of the y coordinate; that is, if P = (x, y), then -P = (x, -y). Note that these two points can be joined by a vertical line. Note that P + ( -P) = P

• P = O.

• 3. To add two points P and Q with different x coordinates, draw a straight line between them and find the third point of intersection R. It is easily seen that there is a unique point R that is the point of intersection (unless the line is tangent to the curve at either P or Q, in which case we take R = P or R = Q, respectively). To form a group structure, we need to define addition on these three points: P + Q = -R. That is, we define P + Q to be the mirror image (with respect to the x axis) of the third point of intersection. Figure 10.4 illustrates this construction.
• 4. The geometric interpretation of the preceding item also applies to two points, P and -P, with the same x coordinate. The points are joined by a vertical line, which can be viewed as also intersecting the curve at the infinity point. We therefore have P + ( -P) = O, which is consistent with item (2).
• 5. To double a point Q, draw the tangent line and find the other point of intersection S. Then Q + Q = 2Q = -S.

• With the preceding list of rules, it can be shown that the set E(a, b) is an abelian group.

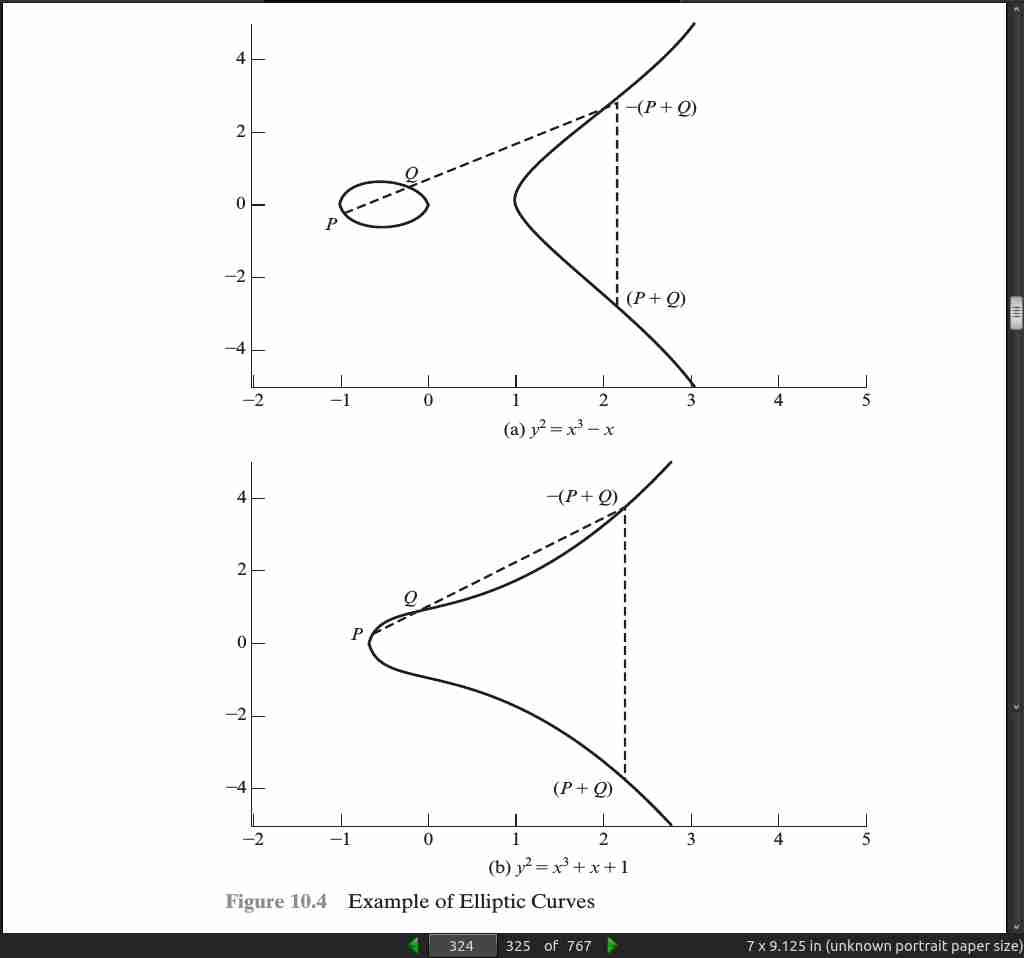
page 325:

• For a prime curve over Z p, we use a cubic equation in which the variables and coefficients all take on values in the set of integers from 0 through p - 1 and in which calculations are performed modulo p. For a binary curve defined over GF(2^m), the variables and coefficients all take on values in GF(2^m) and in calculations are performed over GF(2^m). [FERN99] points out that prime curves are best for software applications, because the extended bit-fiddling operations needed by binary curves are not required; and that binary curves are best for hardware applications, where it takes remarkably few logic gates to create a powerful, fast cryptosystem.

page 332:

page 333:

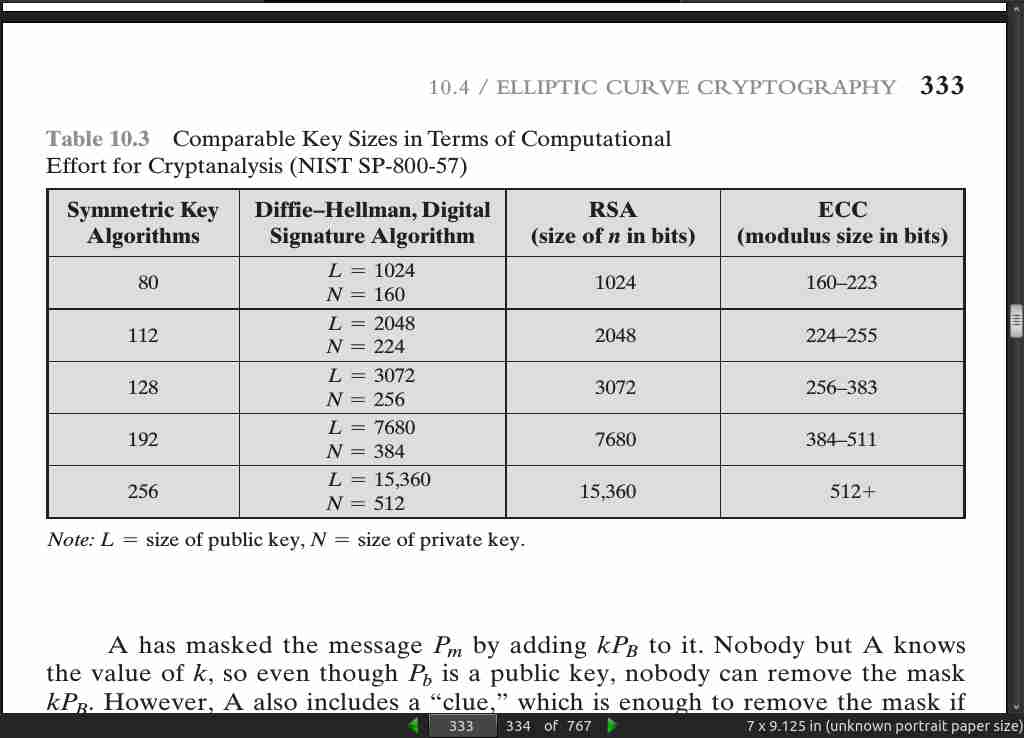
• SP 800-57 recommends that at least through 2030, acceptable key lengths are from 3072 to 14,360 bits for RSA and 256 to 512 bits for ECC. Similarly, the European Union Agency for Network and Information Security (ENISA) recommends in their 2014 report (Algorithms, Key Size and Parameters report—2014, November

2014. minimum key lengths for future system of 3072 bits and 256 bits for RSA and ECC, respectively.

· 11: Cryptographic Hash Functions

page 340:

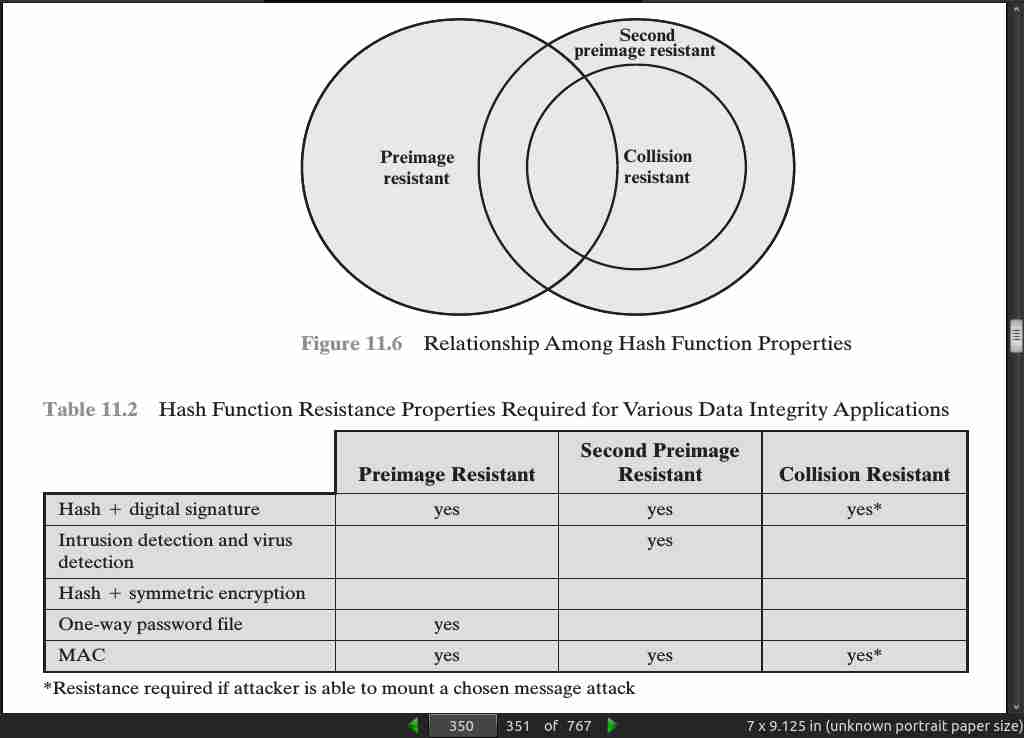
• (a) a data object that maps to a pre-specified hash result (the one-way property) or (b) two data objects that map to the same hash result (the collision-free property).

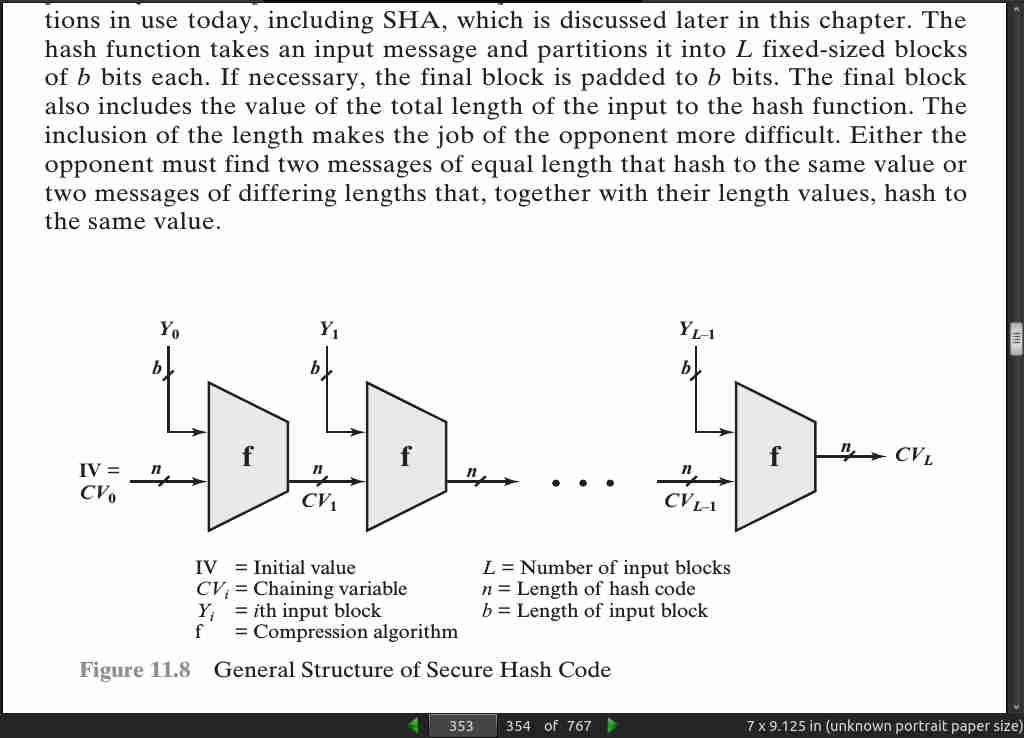
• Typically, the input is padded out to an integer multiple of some fixed length (e.g., 1024 bits), and the padding includes the value of the length of the original mes- sage in bits.

page 343:

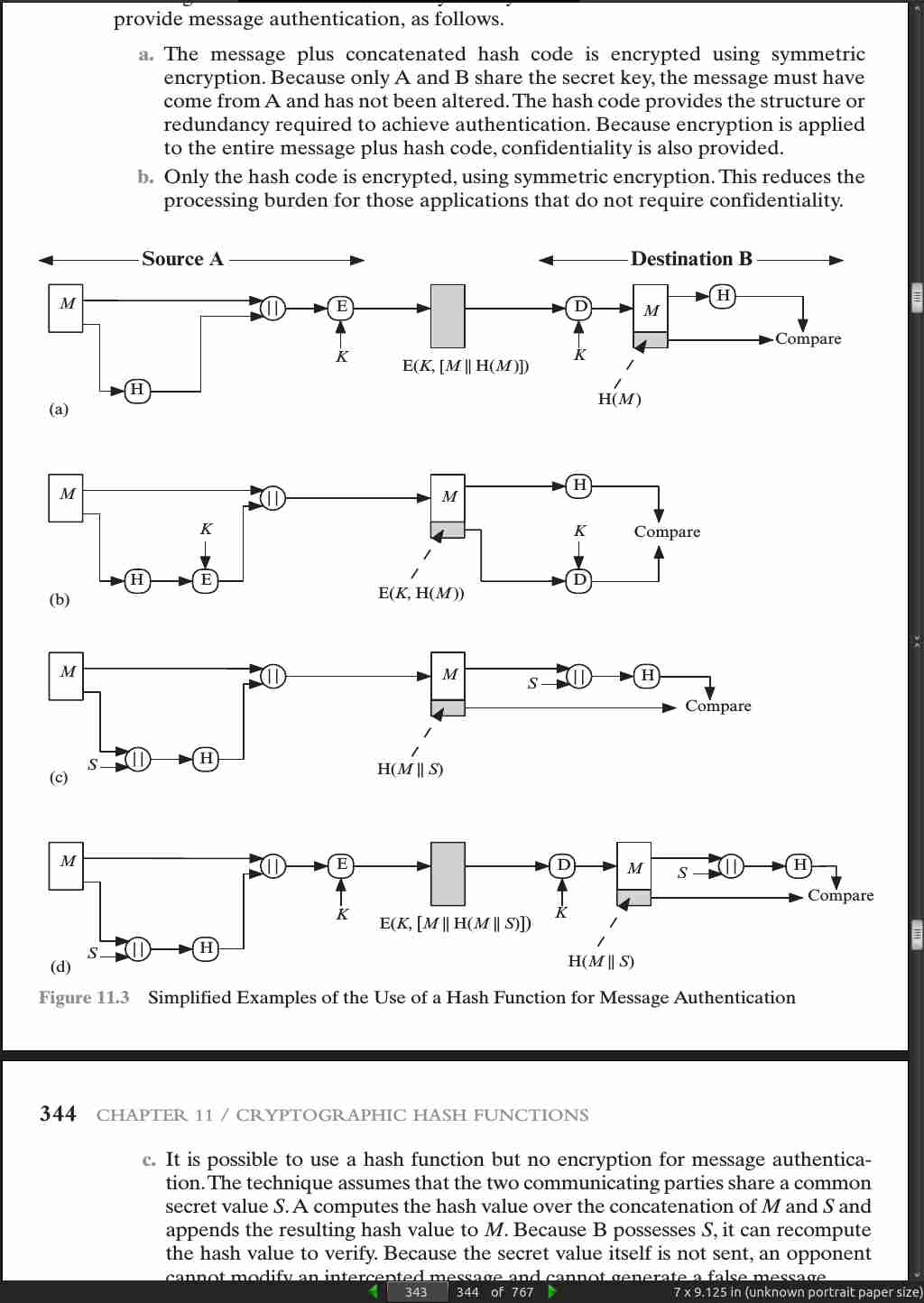
page 344:

• More commonly, message authentication is achieved using a message authentication code (MAC), also known as a keyed hash function. Typically, MACs are used between two parties that share a secret key to authenticate information exchanged between those parties. A MAC function takes as input a secret key and a data block and produces a hash value, referred to as the MAC, which is associated with the protected message. If the integrity of the message needs to be checked, the MAC function can be applied to the message and the result compared with the associated MAC value. An attacker who alters the message will be unable to alter the associated MAC value without knowledge of the secret key.

page 345:

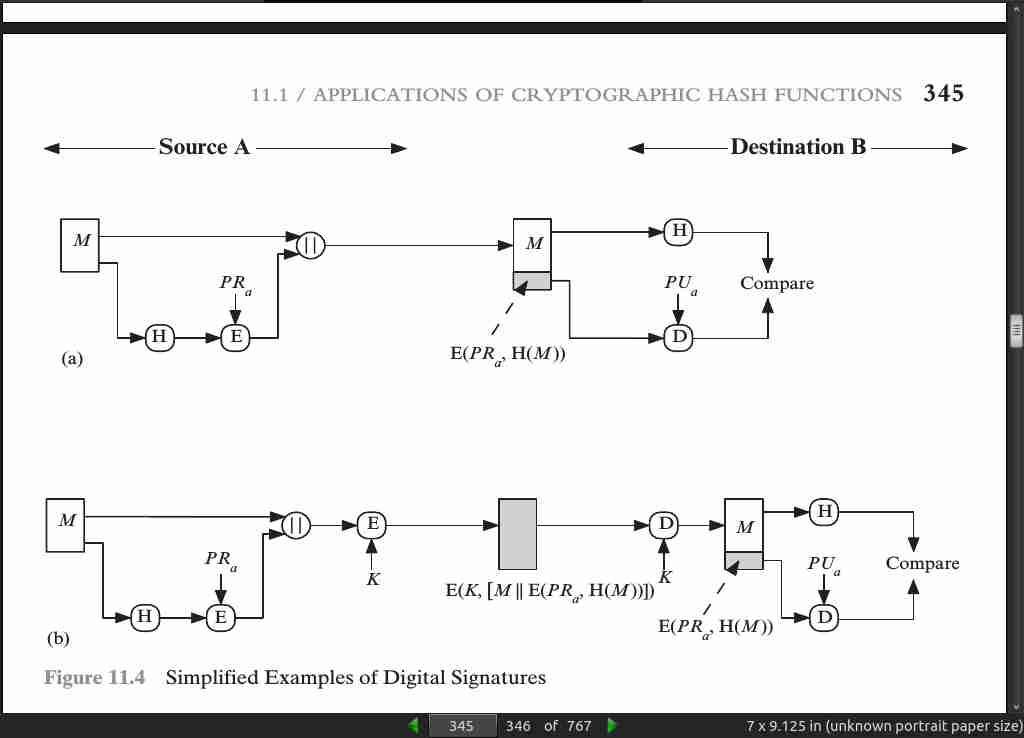
page 348:

• For a hash value h = H(x), we say that x is the preimage of h. That is, x is a data block whose hash value, using the function H, is h. Because H is a many-to-one mapping, for any given hash value h, there will in general be multiple preimages. A collision occurs if we have x != y and H(x) = H(y).

page 349:

• The fifth property, second preimage resistant, guarantees that it is infeasible to find an alternative message with the same hash value as a given message. This pre- vents forgery

page 350:

page 353:

page 356:

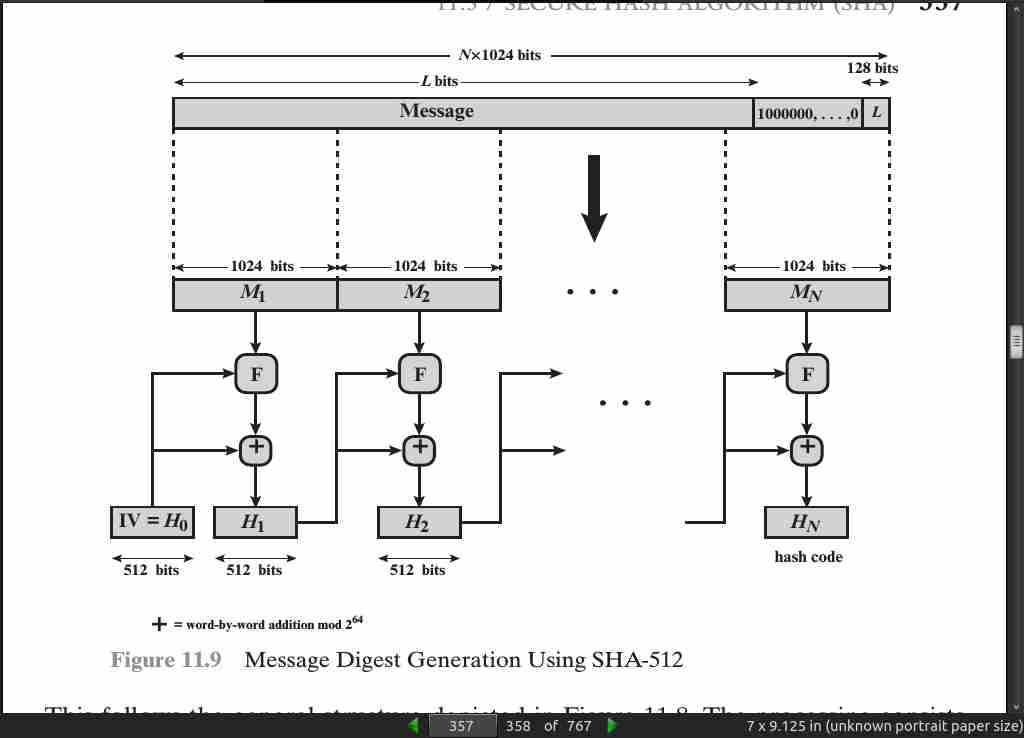
• SHA-1 and SHA-2 are also specified in RFC 6234, which essentially duplicates the material in FIPS 180-3 but adds a C code implementation.

page 357:

page 358:

page 360:

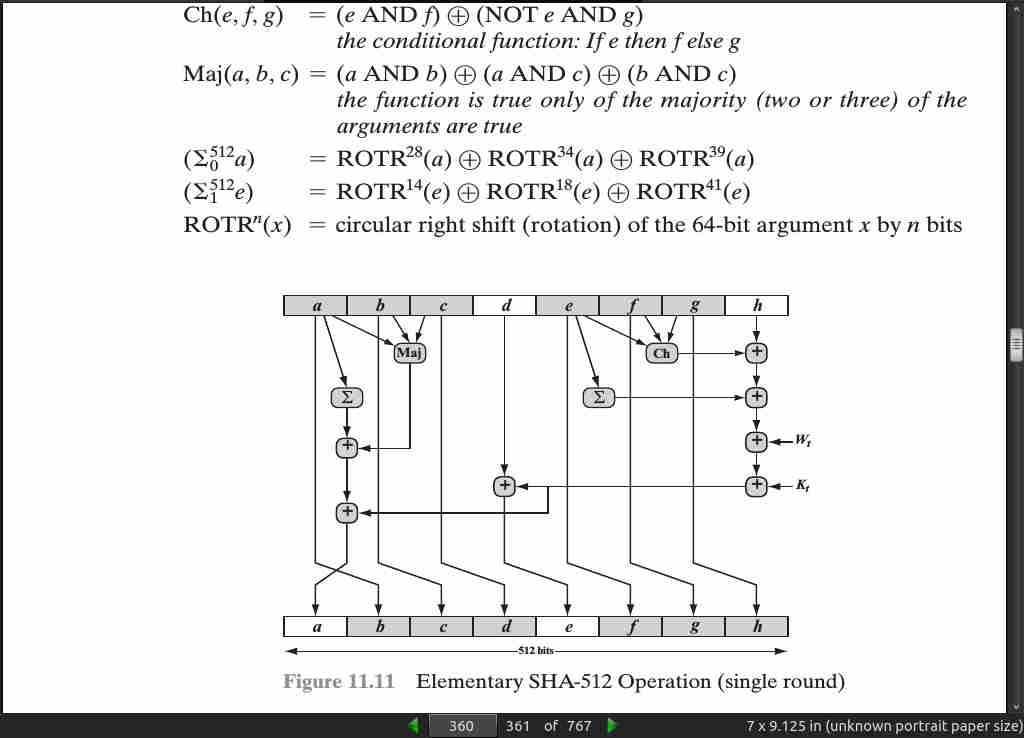
page 361:

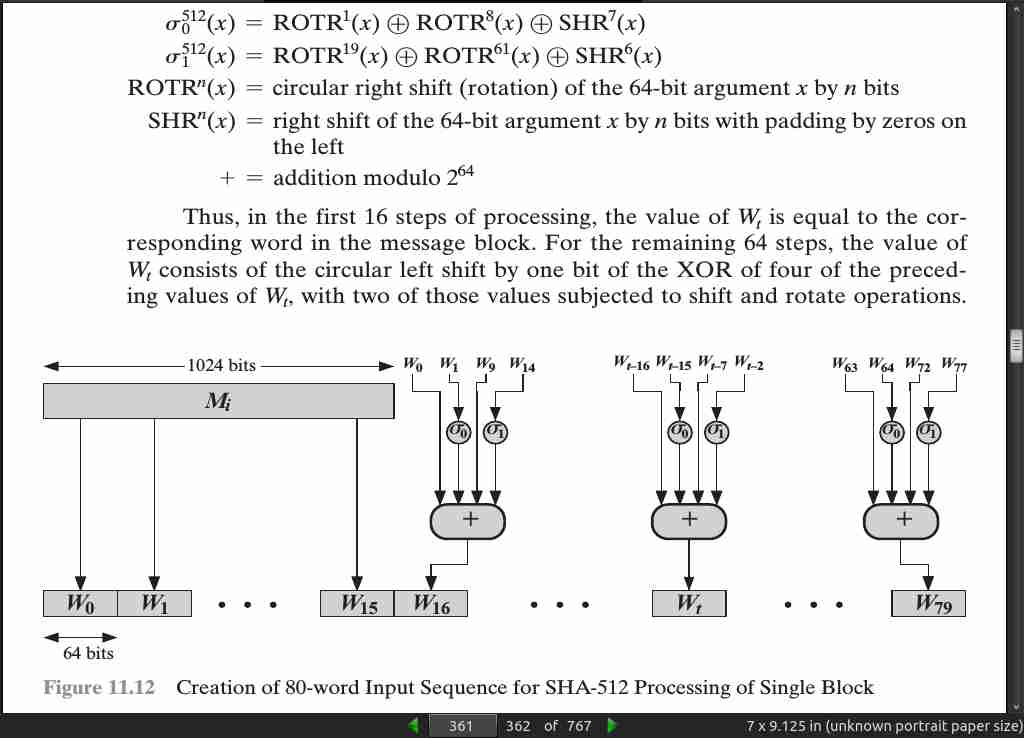
page 362:

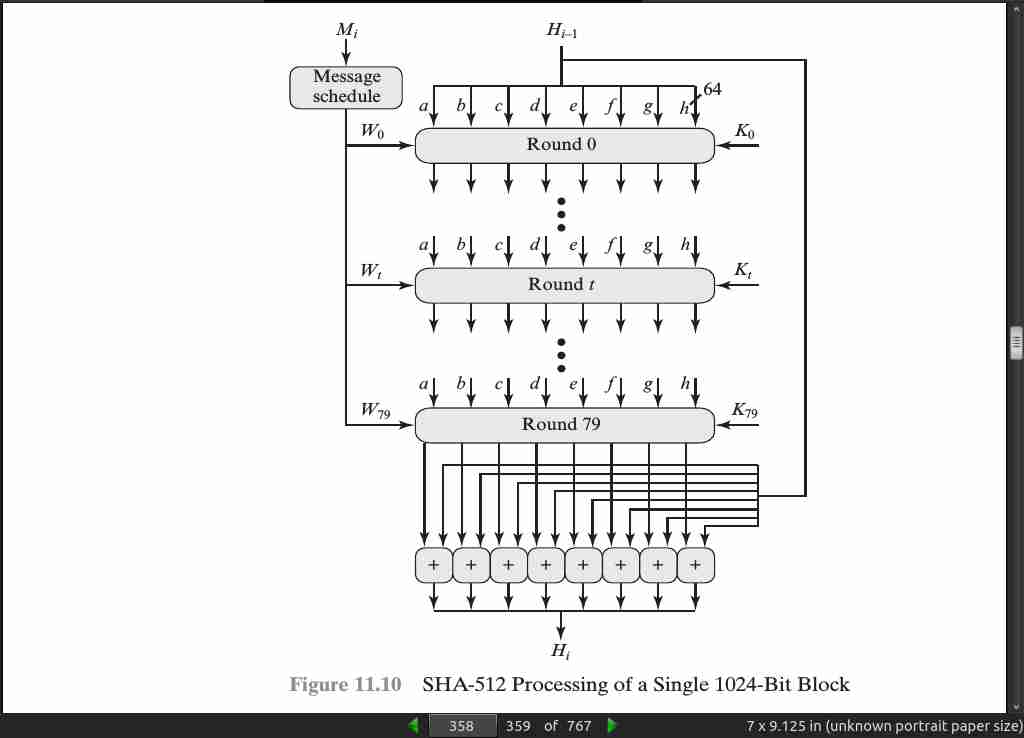
• The SHA-512 algorithm has the property that every bit of the hash code is a function of every bit of the input.

page 363:

· 12: Message Authentication Codes

page 383:

• In summary, message authentication is a procedure to verify that received messages come from the alleged source and have not been altered. Message authentication may also verify sequencing and timeliness. A digital signature is an authentication technique that also includes measures to counter repudiation by the source.

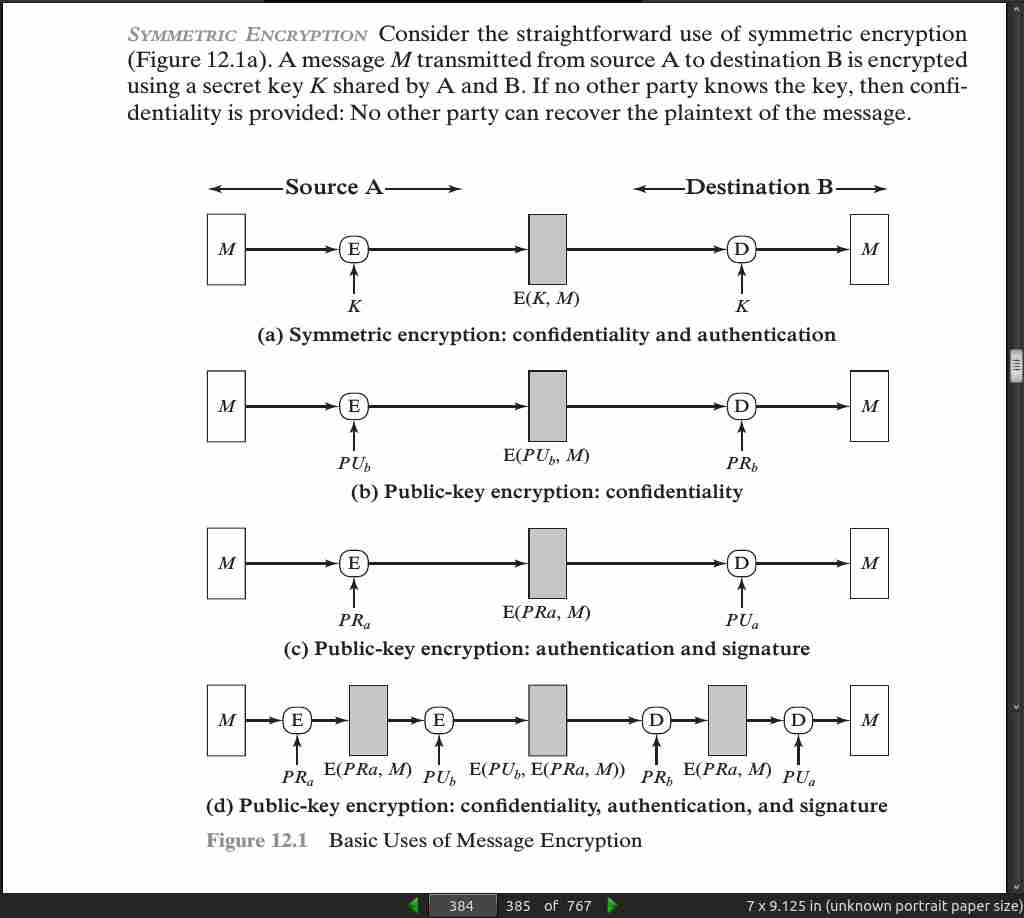
page 384:

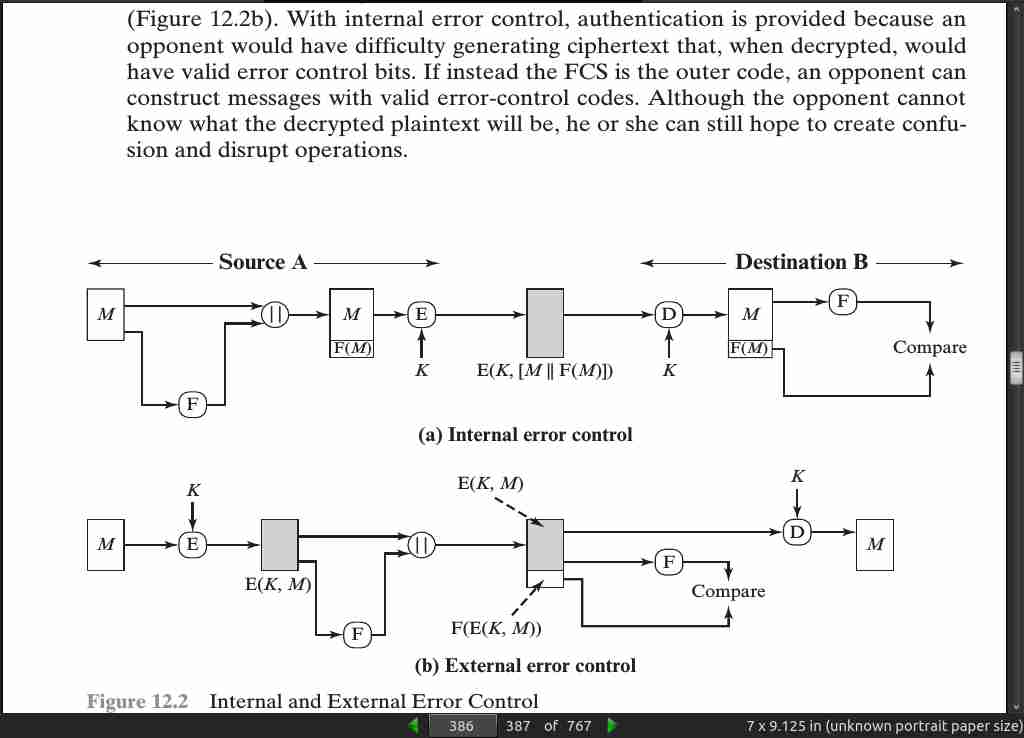
page 386:

page 388:

• An alternative authentication technique involves the use of a secret key to generate a small fixed-size block of data, known as a cryptographic checksum or MAC, that is appended to the message.

page 389:

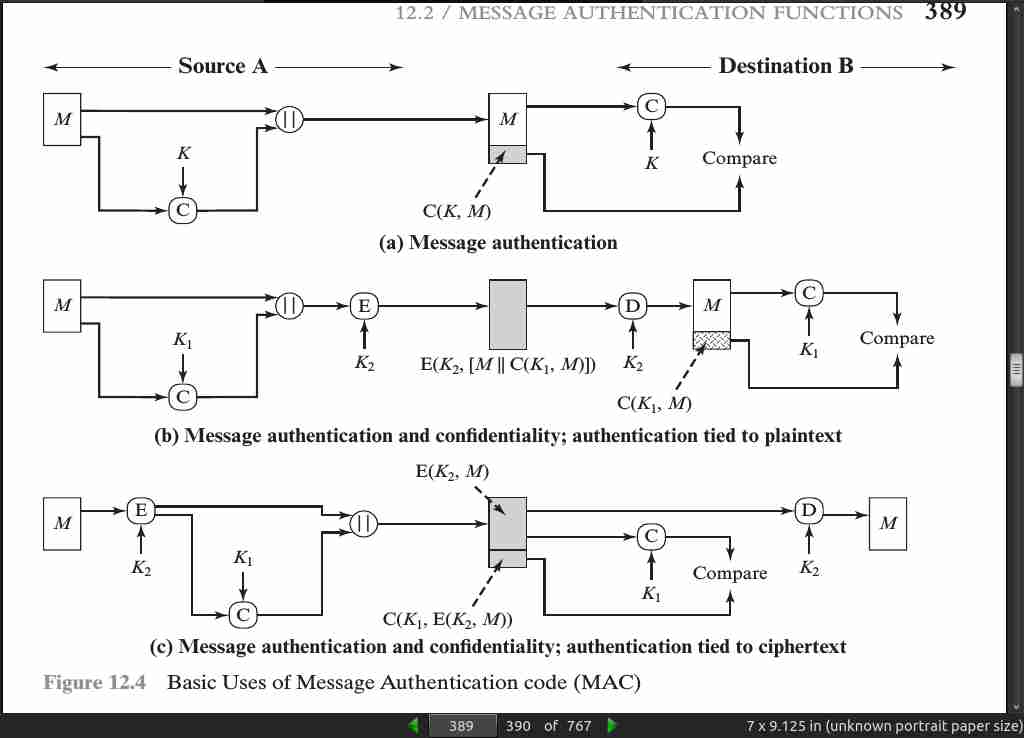
page 390:

• Typically, it is preferable to tie the authentication directly to the plaintext, so the method of Figure 12.4b is used.

• Finally, note that the MAC does not provide a digital signature, because both sender and receiver share the same key.

page 394:

• Suppose the key size is k bits and that the attacker has one known text-tag pair. Then the attacker can compute the n-bit tag on the known text for all possible keys. … To summarize, the level of effort for brute-force attack on a MAC algorithm can be expressed as min(2^k, 2^n ). The assessment of strength is similar to that for symmetric encryption algorithms. It would appear reasonable to require that the key length and tag length satisfy a relationship such as min(k, n) >= N, where N is perhaps in the range of 128 bits.

page 398:

• if speed is a concern, it is fully acceptable to use MD5 rather than SHA-1 as the embedded hash function for HMAC.

page 414:

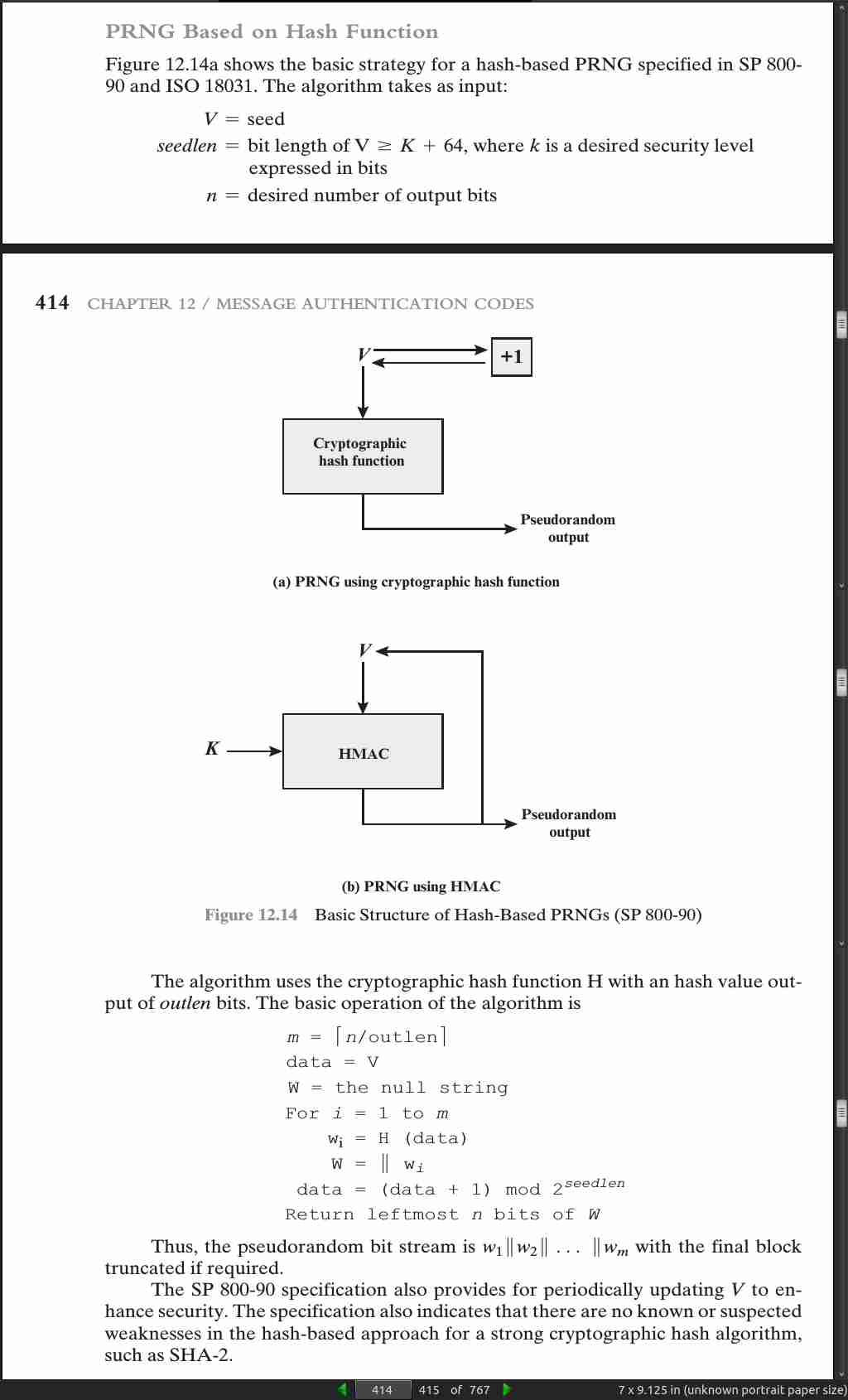
· 13: Digital Signatures

page 421:

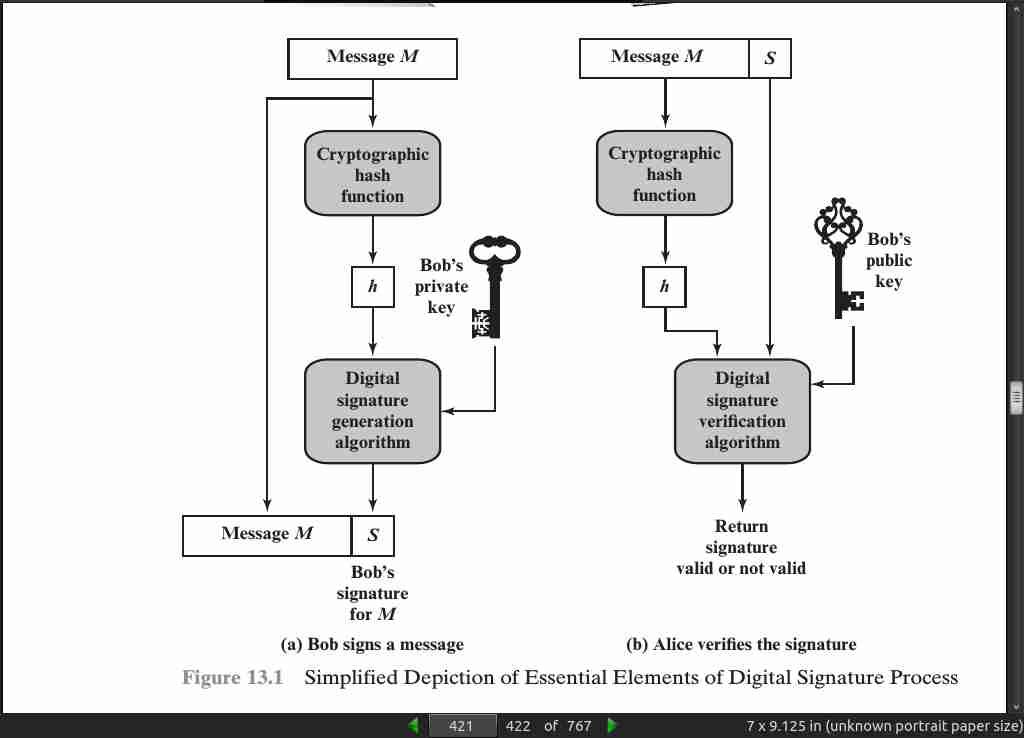
page 422:

• For example, suppose that John sends an authenticated message to Mary, using one of the schemes of Figure 12.1. Consider the following disputes that could arise.

1. Mary may forge a different message and claim that it came from John. Mary
would simply have to create a message and append an authentication code using
the key that John and Mary share.
2. John can deny sending the message. Because it is possible for Mary to forge
a message, there is no way to prove that John did in fact send the message.

• In situations where there is not complete trust between sender and receiver, something more than authentication is needed. The most attractive solution to this problem is the digital signature.

page 427:

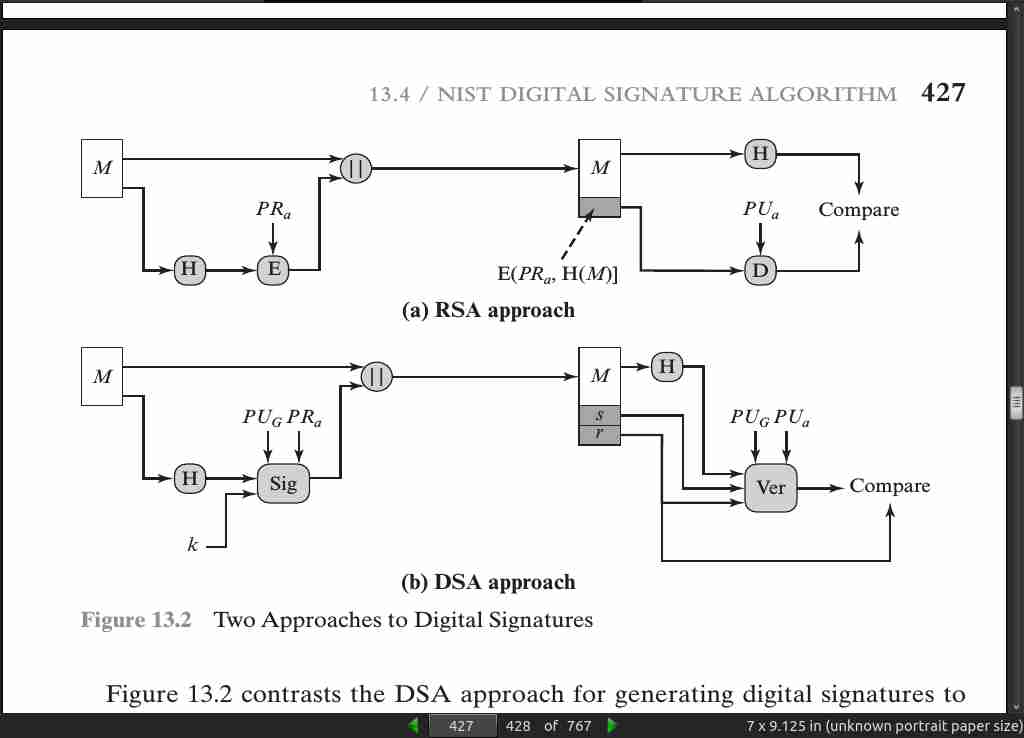
page 428:

page 429:

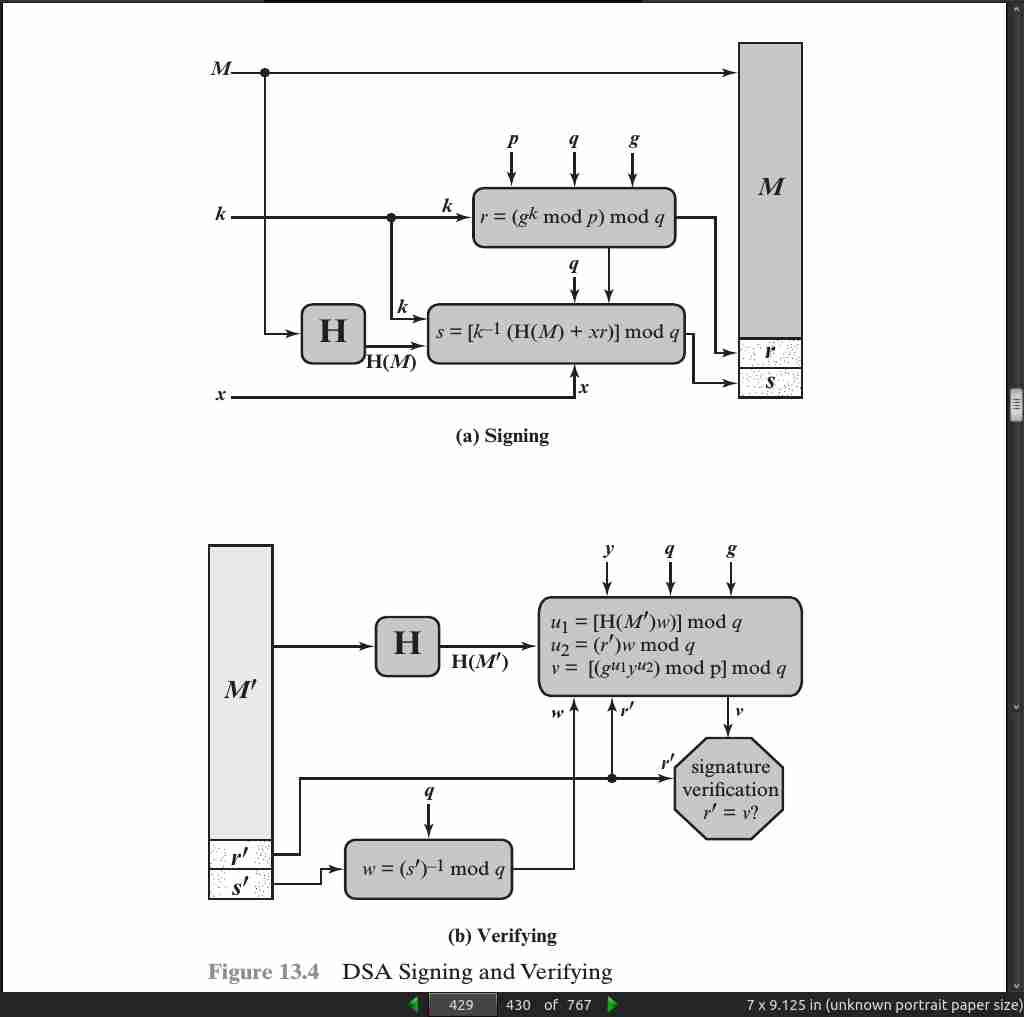
page 432:

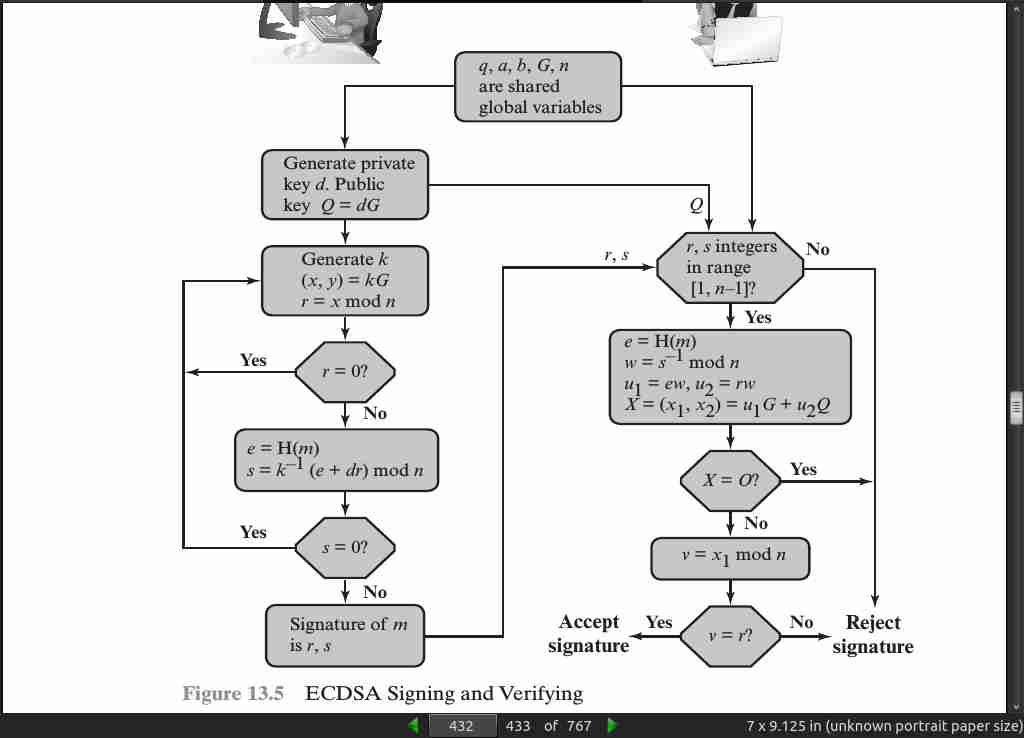
· 14: Key Management and Distribution

page 442:

• For symmetric encryption to work, the two parties to an exchange must share the same key, and that key must be protected from access by others. Furthermore, frequent key changes are usually desirable to limit the amount of data compromised if an attacker learns the key. Therefore, the strength of any cryptographic system rests with the key distribution technique, a term that refers to the means of delivering a key to two parties who wish to exchange data without allowing others to see the key.

page 448:

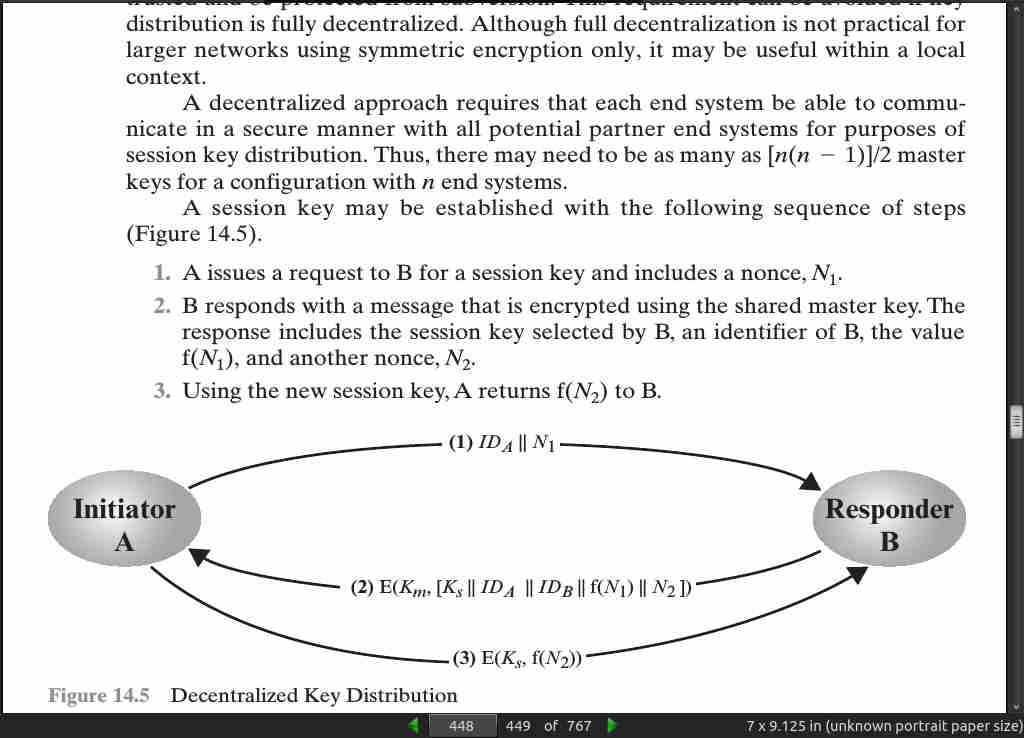
page 451:

• If A wishes to communicate with B, the following procedure is employed:

1. A generates a public/private key pair {PUa, PR a} and transmits a message to
B consisting of PUa and an identifier of A, ID A.
2. B generates a secret key, K s, and transmits it to A, which is encrypted
with A’s public key.
3. A computes D(PR a, E(PUa, K s)) to recover the secret key. Because only A
can decrypt the message, only A and B will know the identity of K s.
4. A discards PUa and PR a and B discards PUa.  A and B can now securely
communicate using conventional encryption and the session key Ks. At the
completion of the exchange, both A and B discard K s.  Despite its simplicity,
this is an attractive protocol.

page 453:

page 460:

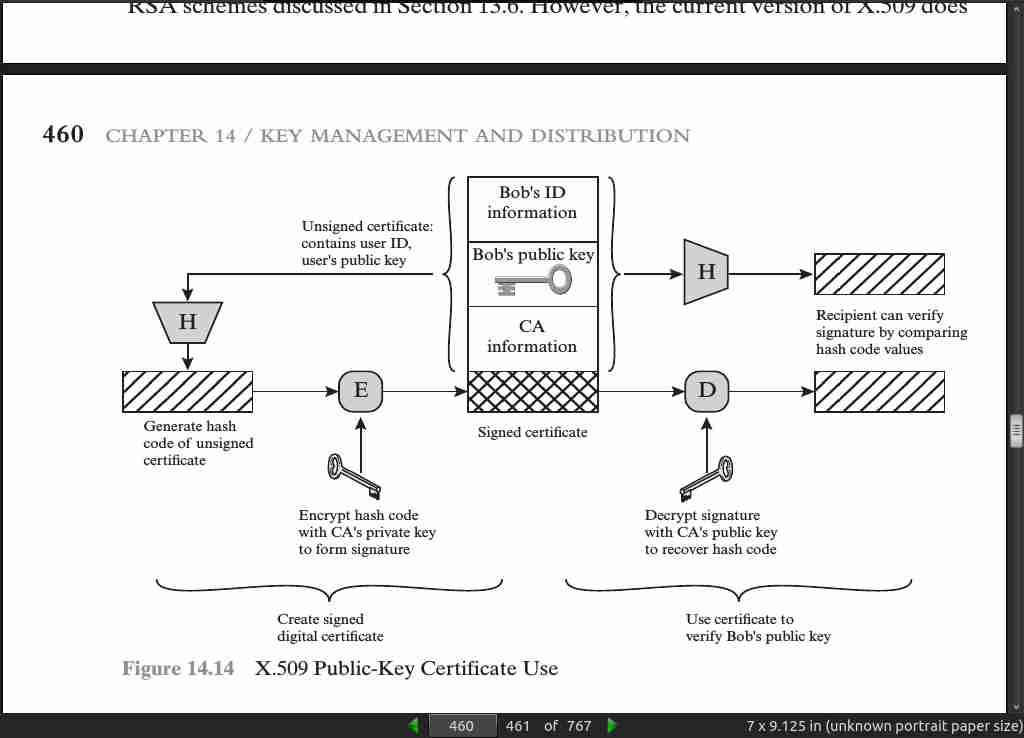
· 15: User Authentication

page 481:

• Mutual authentication:

1. A -> B:     ID_A || N_a
2. B -> KDC:   ID_B || N_b || E(K_b, [ID_A || N_a || T_b])
3. KDC -> A:   E(K_a, [ID_B || N_a || K_s || T_b]) || E(K_b, [ID_A || K_s || T_b]) || N_b
4. A -> B:     E(K_b, [ID_A || K_s || T_b]) || E(K_s, N_b)

|| = concatenate
KDC = Key Distribution Center
N = Nonce
K = Key
T = Timestamp
ID = Identifier

page 488:

page 489:

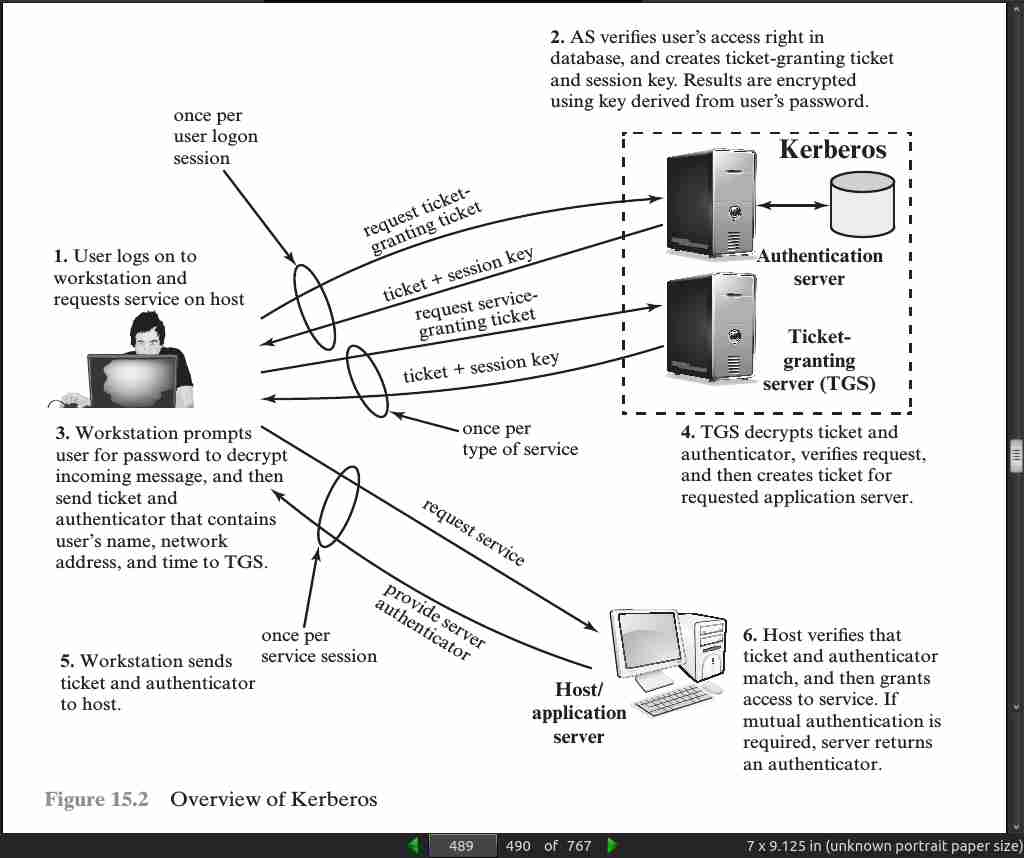
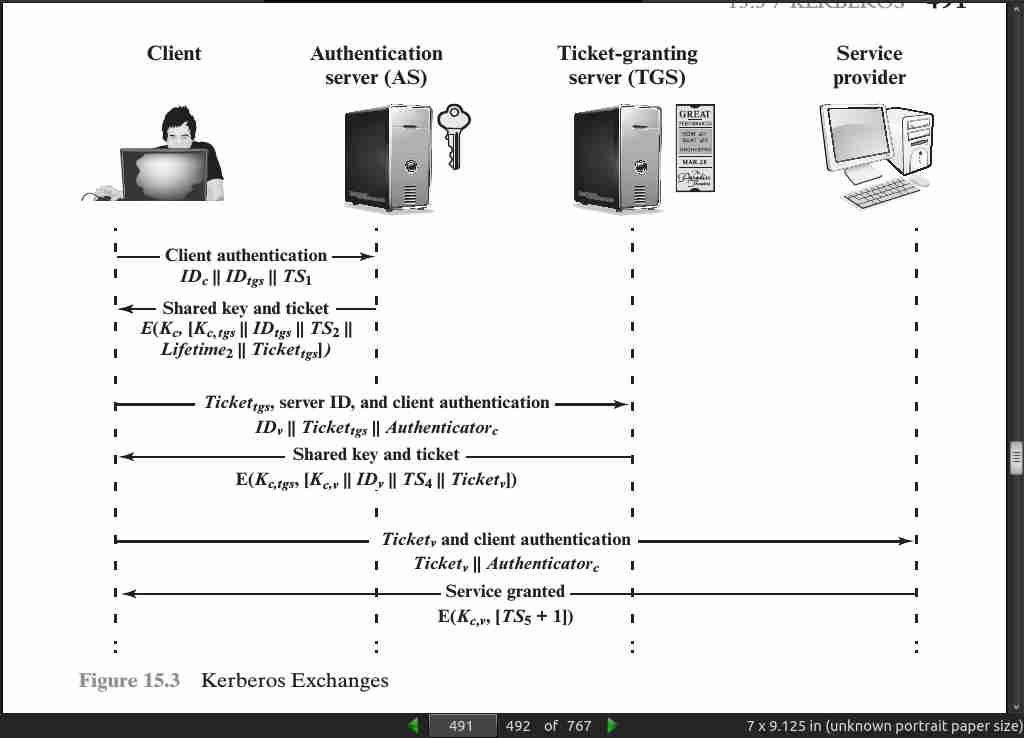
page 491:

· 16: Network Access Control and Cloud Security

page 532:

• Software as a Service (SaaS), Infrastructure as a Service (IaaS), and Platform as a Service (PaaS)

· 17: Transport-Level Security

page 549:

page 556:

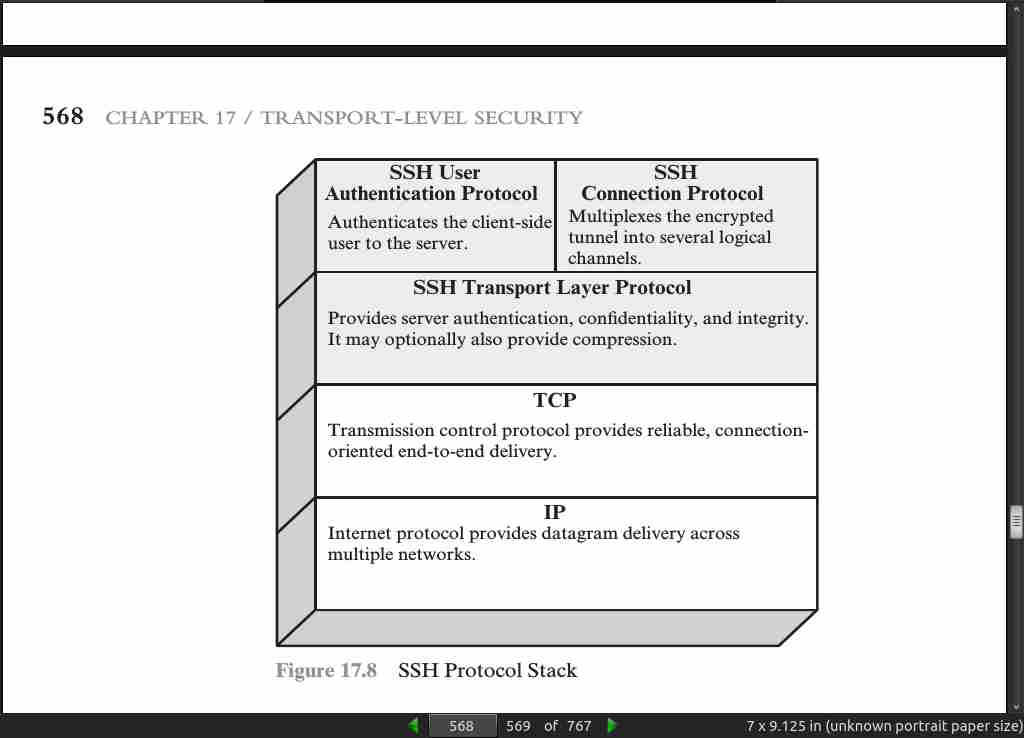
page 568:

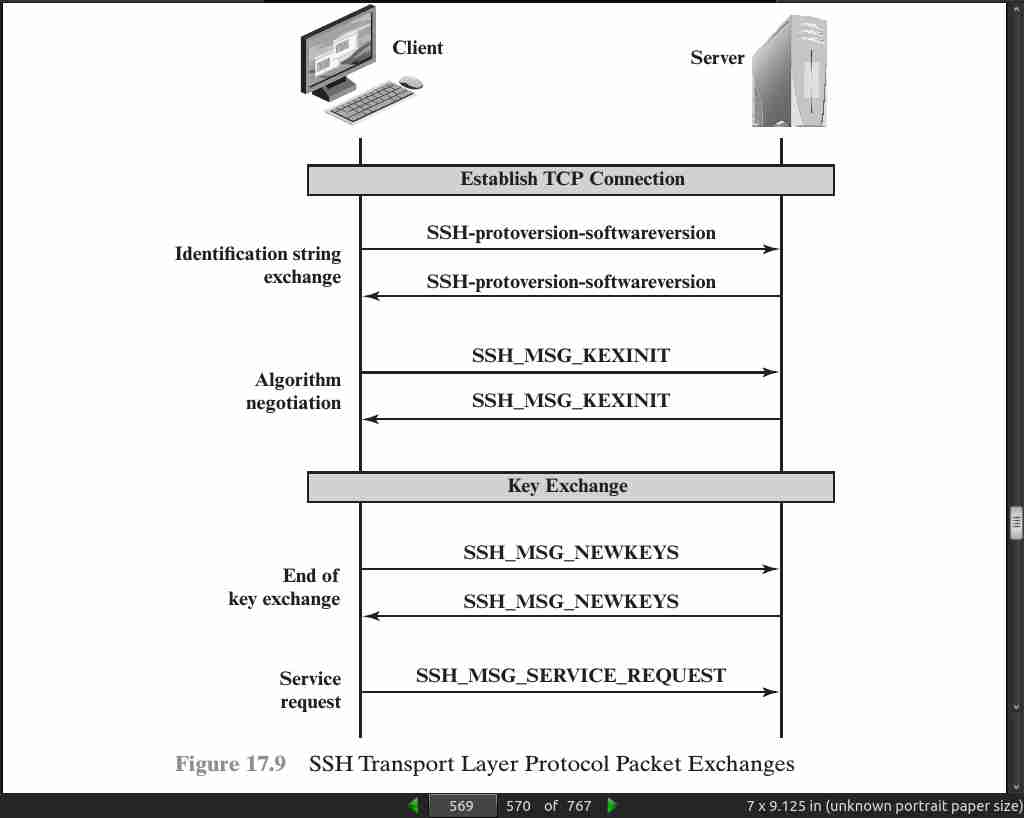
page 569:

page 570:

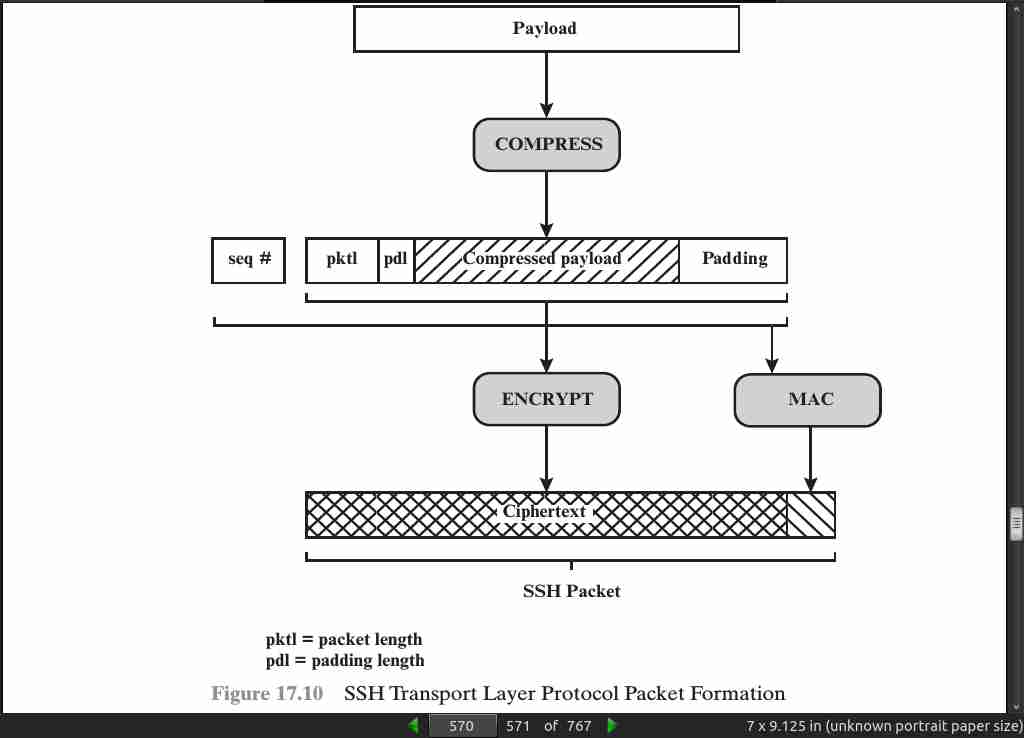
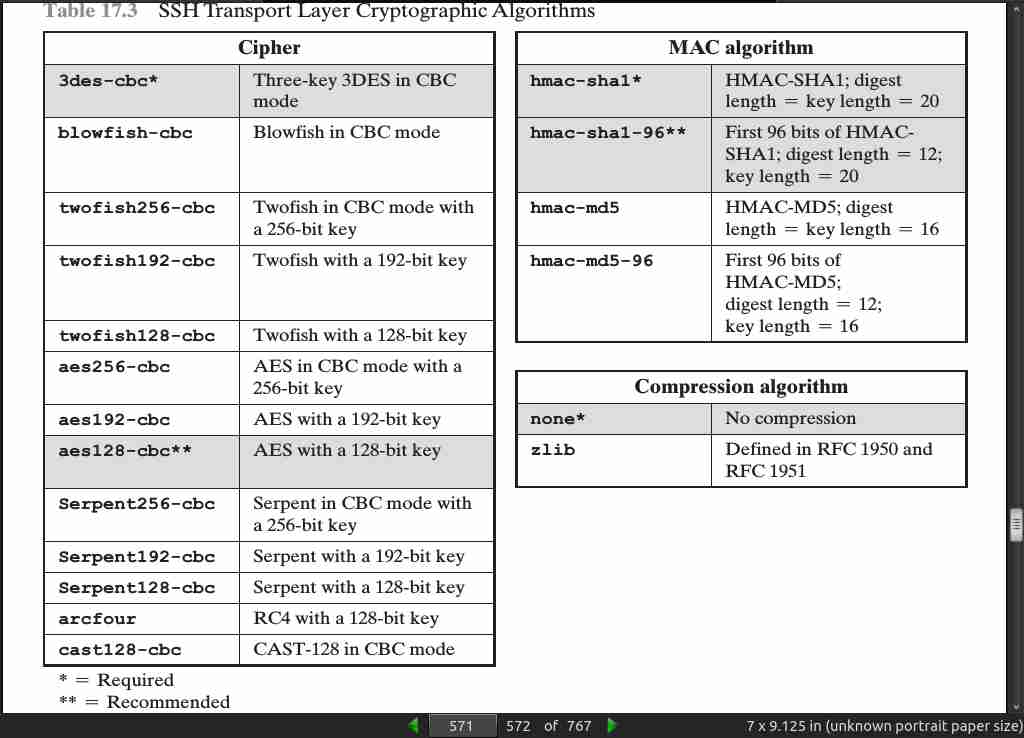
page 571:

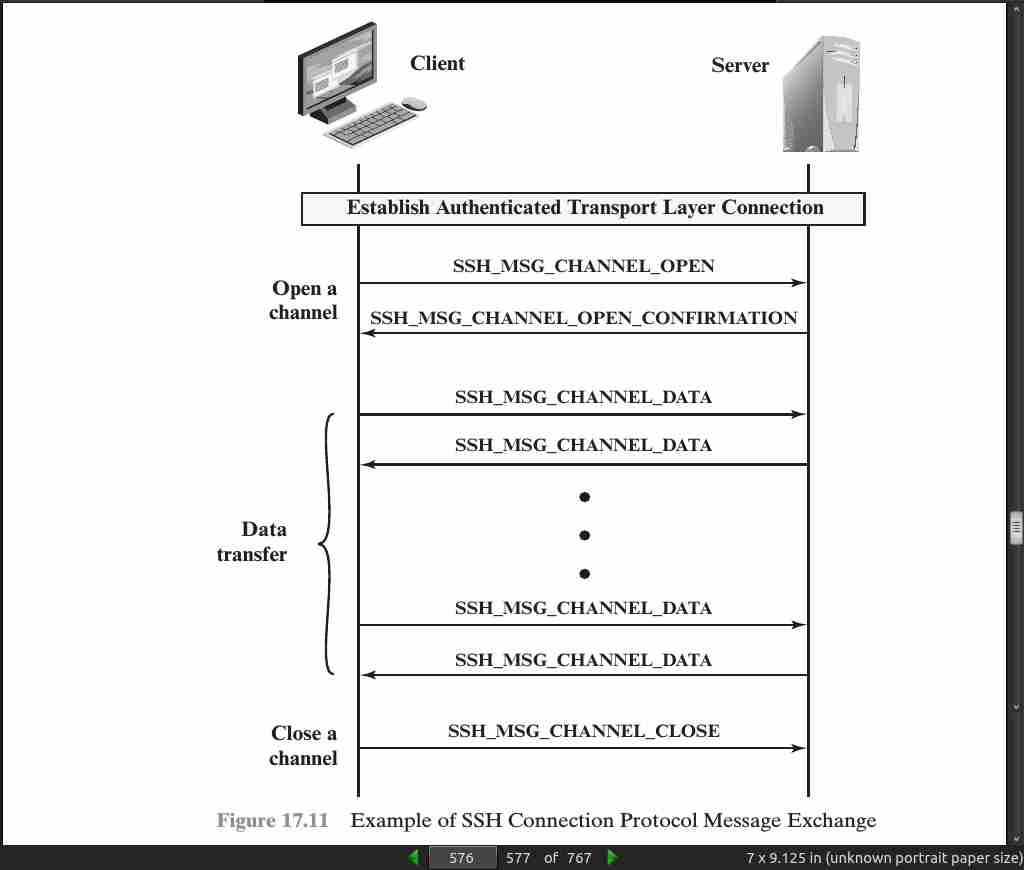
page 576:

· 18: Wireless Network Security

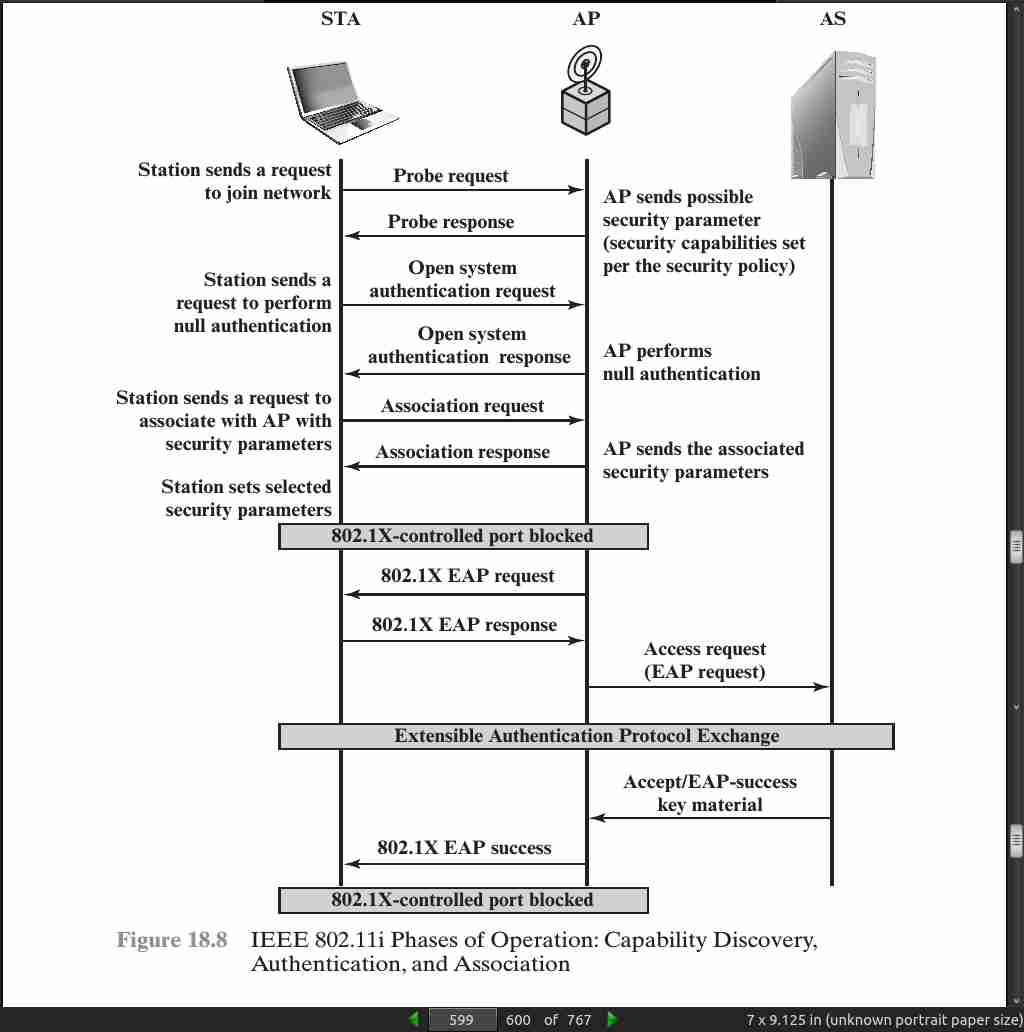
page 599:

· 19: Electronic Mail Security

page 631:

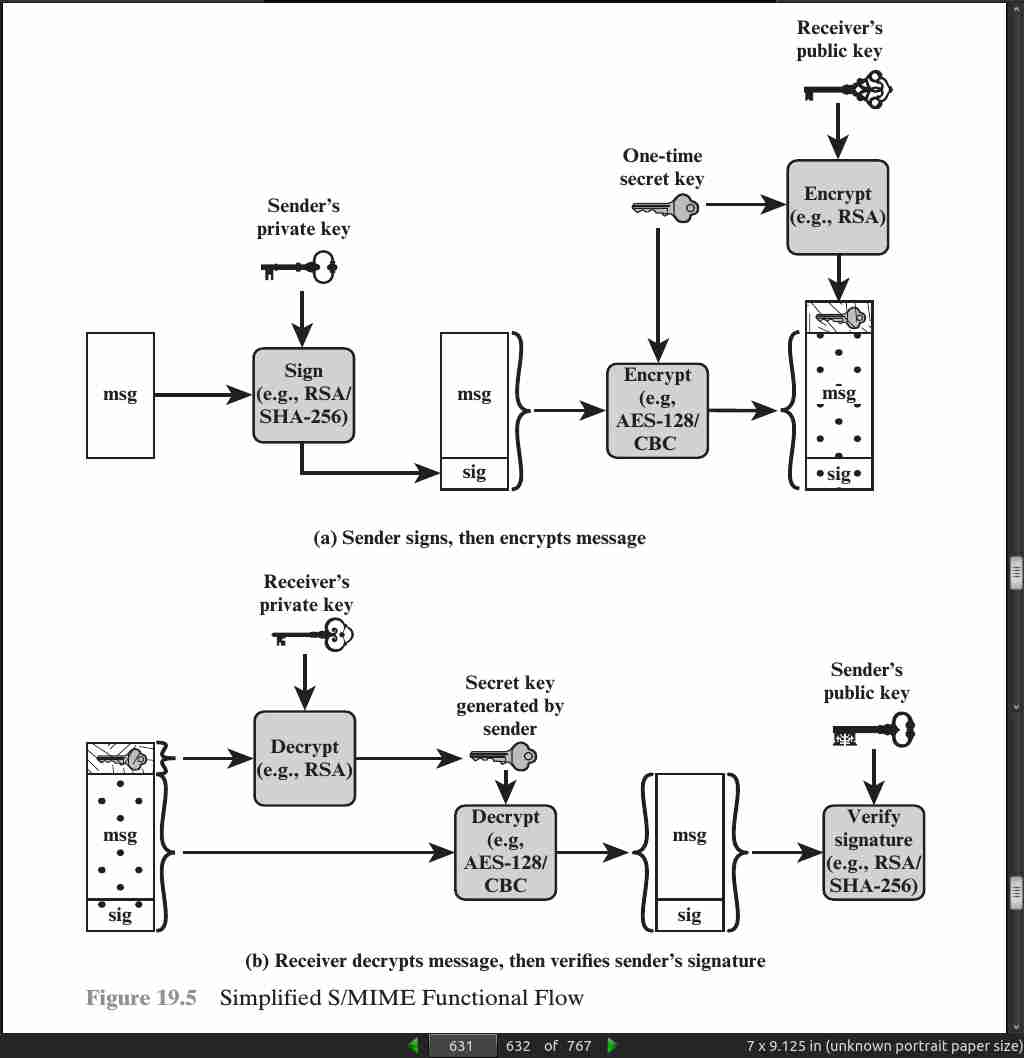
page 638:

• Whereas X.509 certificates are trusted if there is a valid PKIX chain to a trusted root, an OpenPGP public key is trusted if it is signed by another OpenPGP public key that is trusted by the recipient. This is called the Web-of-Trust.

• OpenPGP does not include the sender’s public key with each message, so it is necessary for recipients of OpenPGP messages to sepa- rately obtain the sender’s public key in order to verify the message.

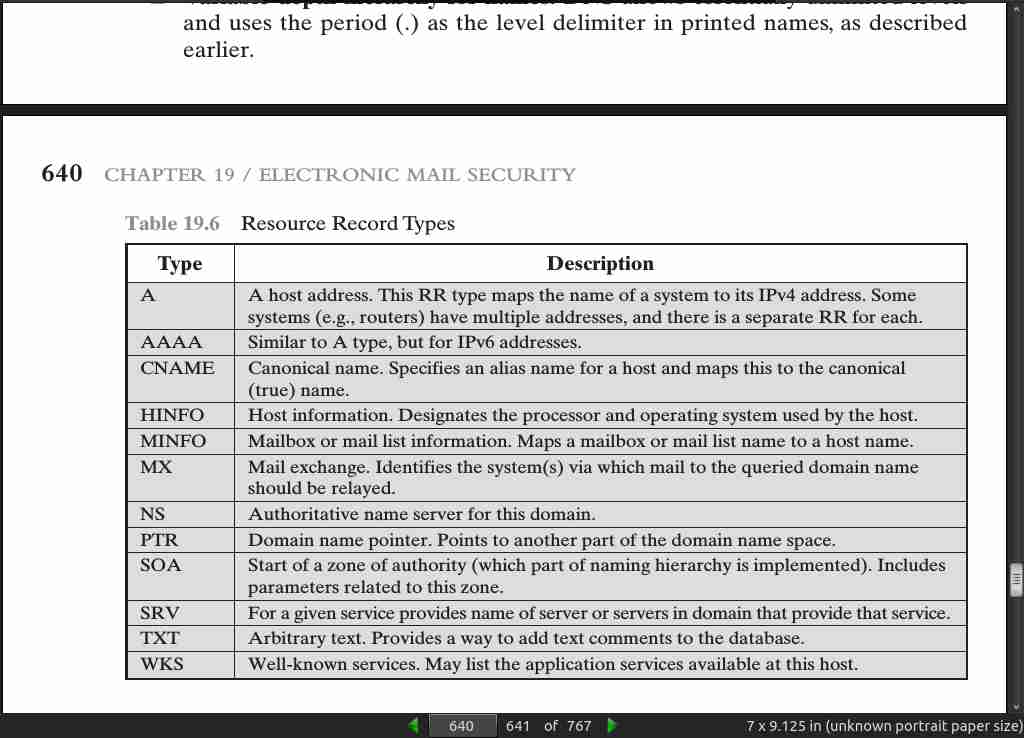
page 640:

page 643:

• DANE is a protocol to allow X.509 certificates, commonly used for Transport Layer Security (TLS), to be bound to DNS names using DNSSEC. It is proposed in RFC 6698 as a way to authenticate TLS client and server entities without a certificate authority (CA).

• The rationale for DANE is the vulnerability of the use of CAs in a global PKI system. Every browser developer and operating system supplier maintains a list of CA root certificates as trust anchors. These are called the software’s root certifi- cates and are stored in its root certificate store. The PKIX procedure allows a cer- tificate recipient to trace a certificate back to the root. So long as the root certificate remains trustworthy, and the authentication concludes successfully, the client can proceed with the connection.

• However, if any of the hundreds of CAs operating on the Internet is compro- mised, the effects can be widespread. The attacker can obtain the CA’s private key, get issued certificates under a false name, or introduce new bogus root certificates into a root certificate store. There is no limitation of scope for the global PKI and a compromise of a single CA damages the integrity of the entire PKI system. In addition, some CAs have engaged in poor security practices.

· 20: IP Security

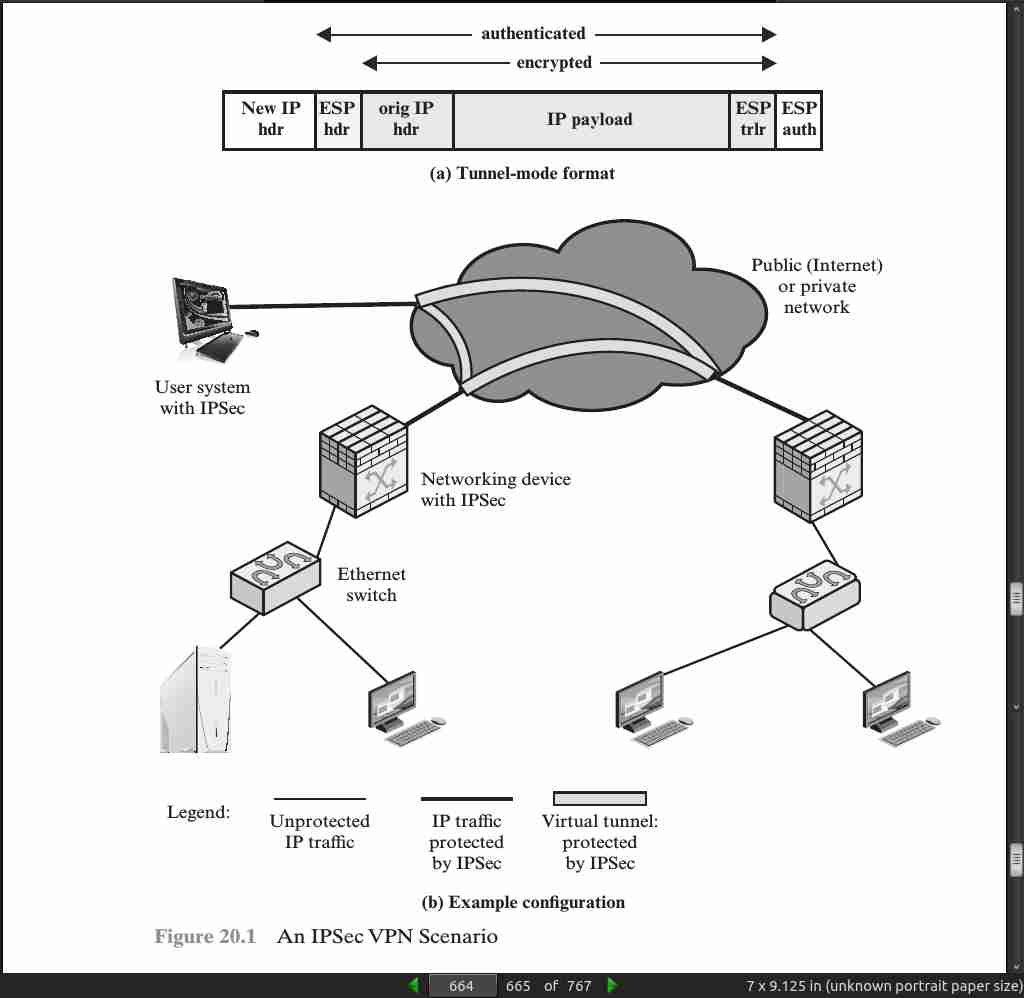
page 664:

page 668:

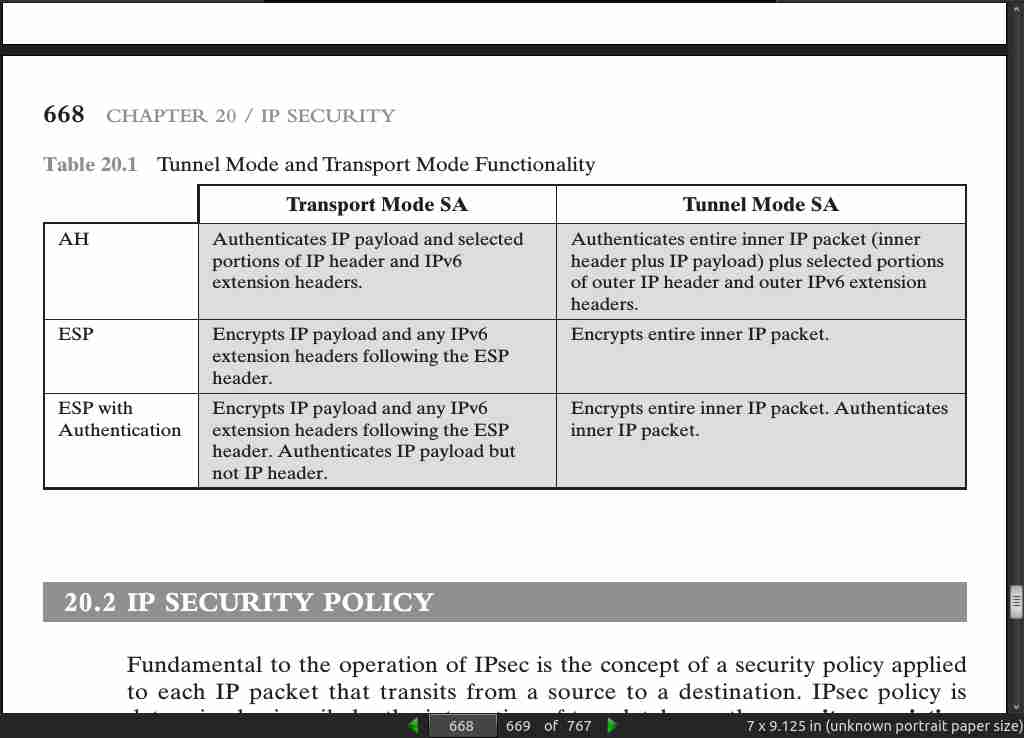
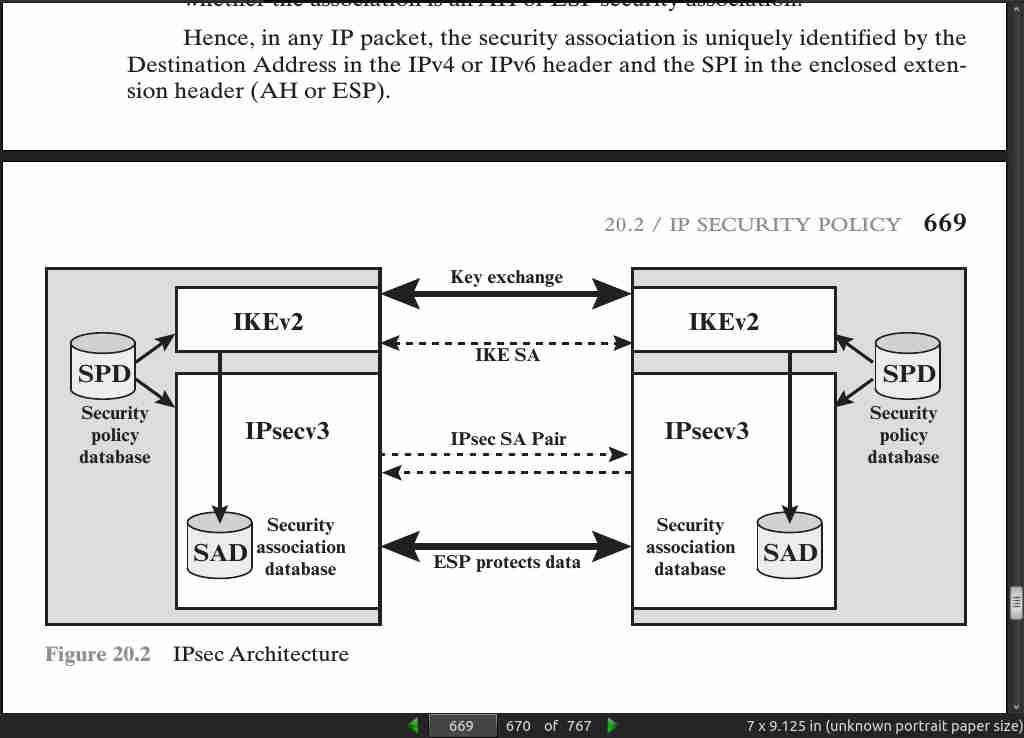
• IPsec policy is determined primarily by the interaction of two databases, the security association database (SAD) and the security policy database (SPD).

page 669:

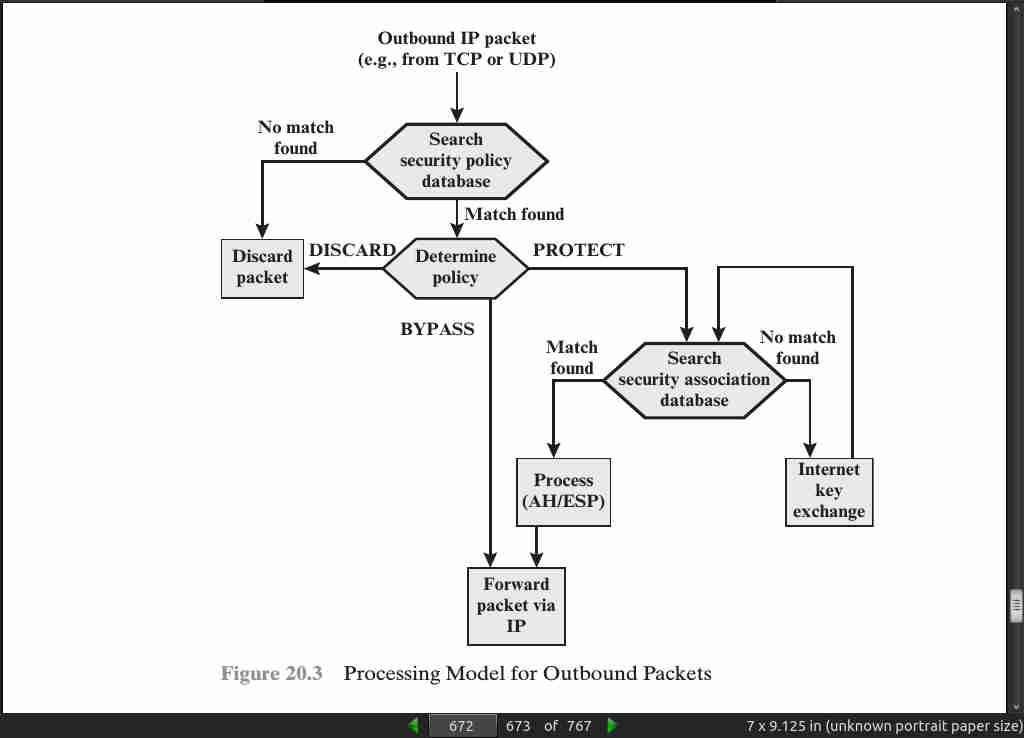
page 672:

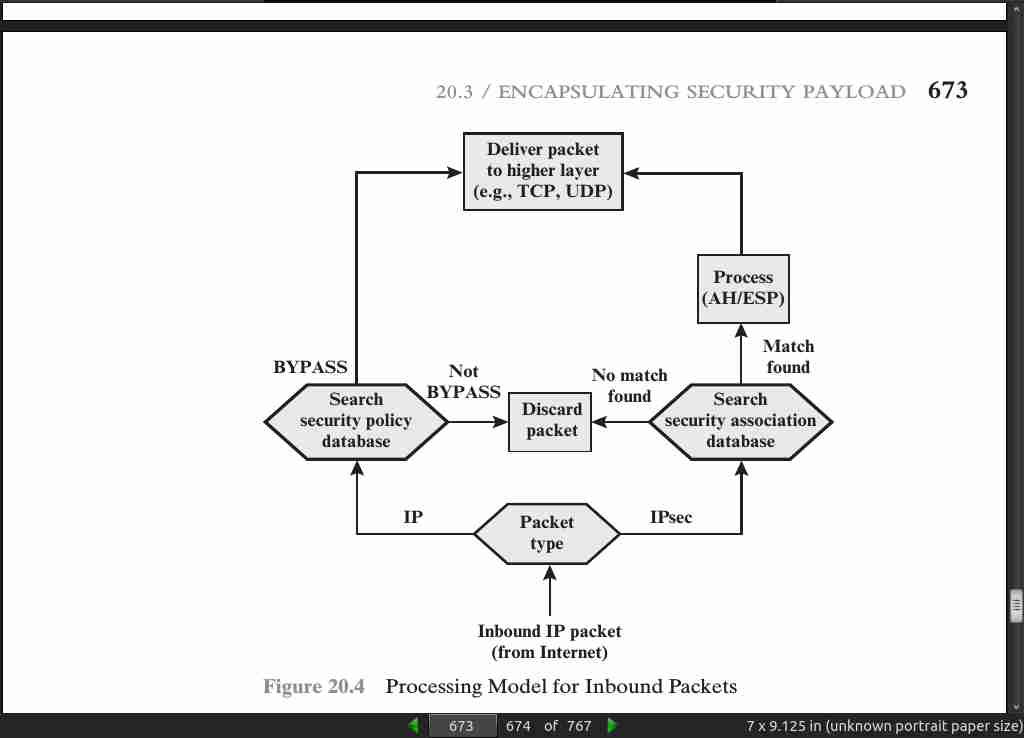
page 673:

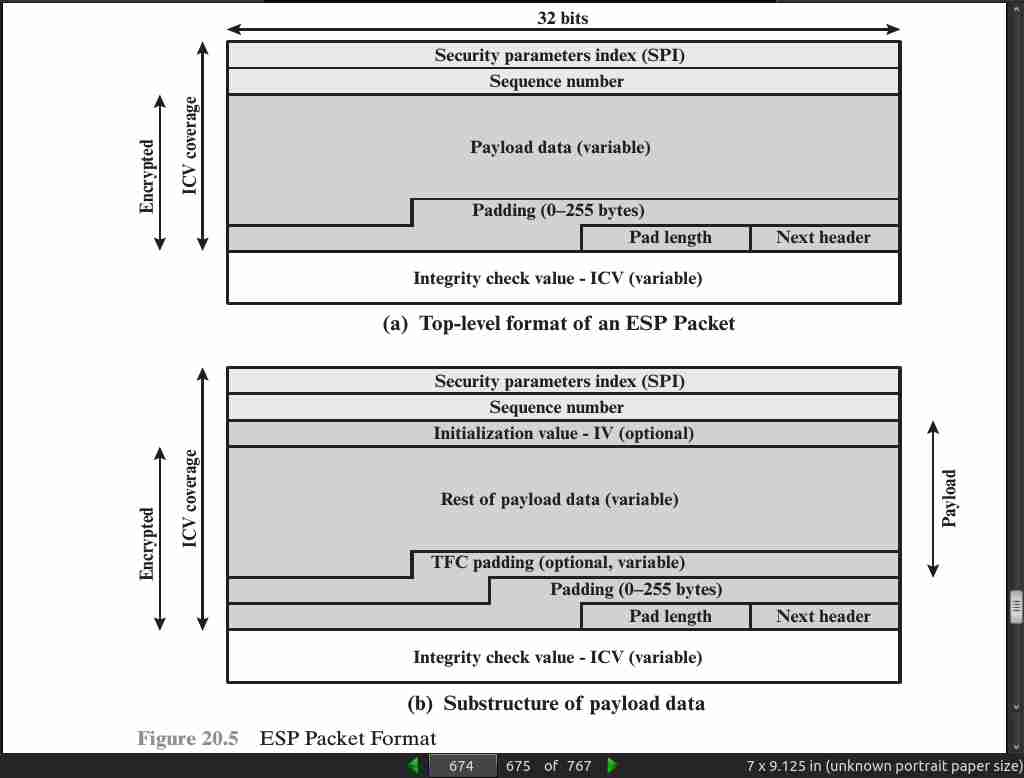
page 674:

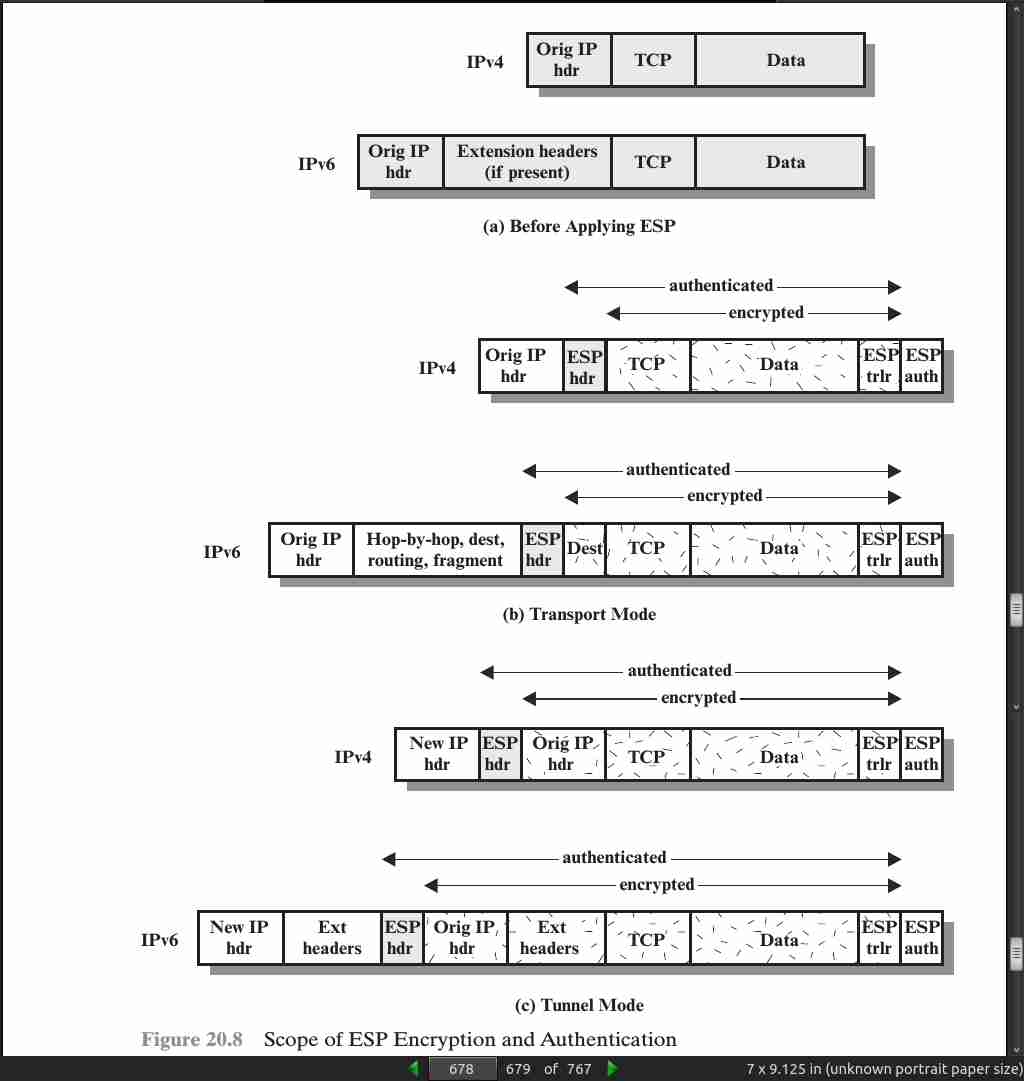
page 678:

• Transport and Tunnel modes.

page 679:

• Whereas the transport mode is suitable for protecting connections between hosts that support the ESP feature, the tunnel mode is useful in a configuration that includes a firewall or other sort of security gateway that protects a trusted network from external networks. In this latter case, encryption occurs only between an external host and the security gateway or between two security gateways. This relieves hosts on the internal network of the processing burden of encryption and simplifies the key distribution task by reducing the number of needed keys. Further, it thwarts traffic analysis based on ultimate destination.

page 680:

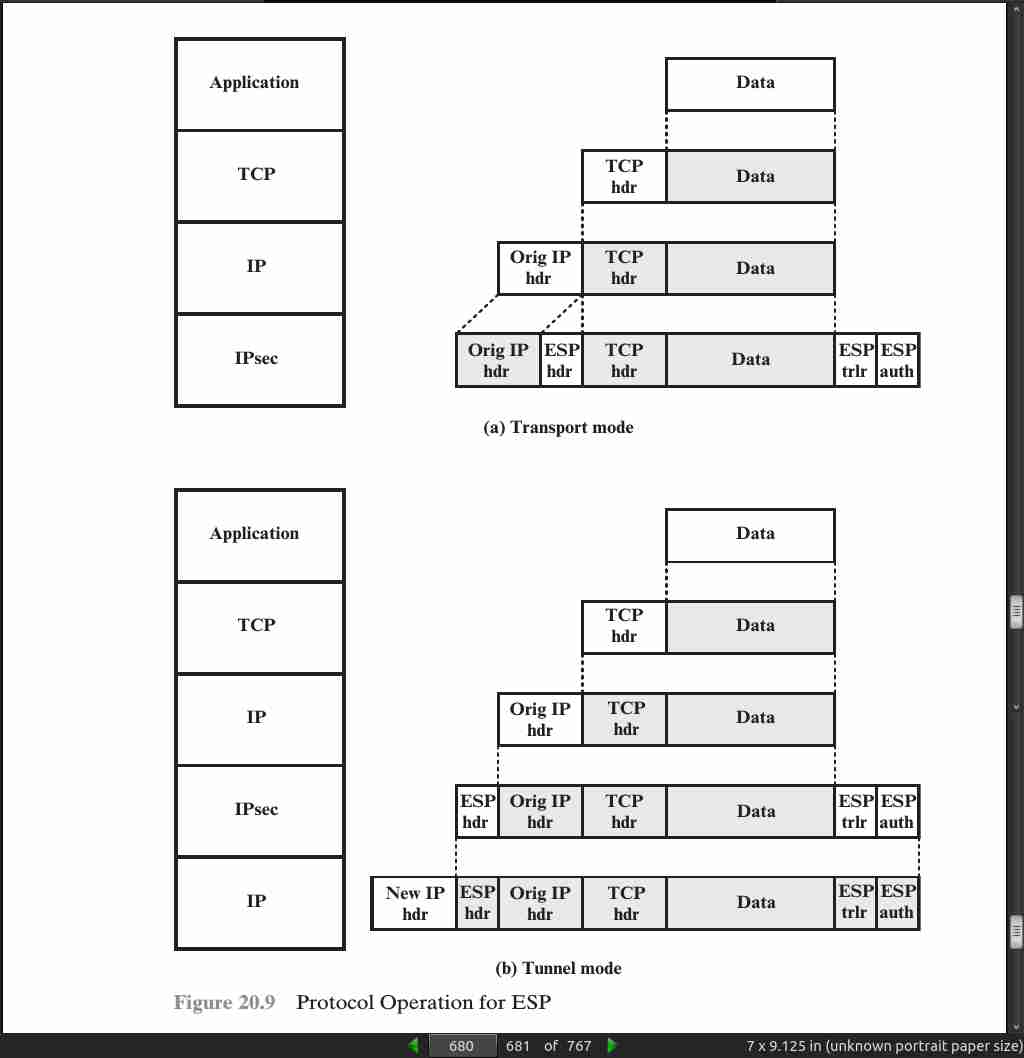
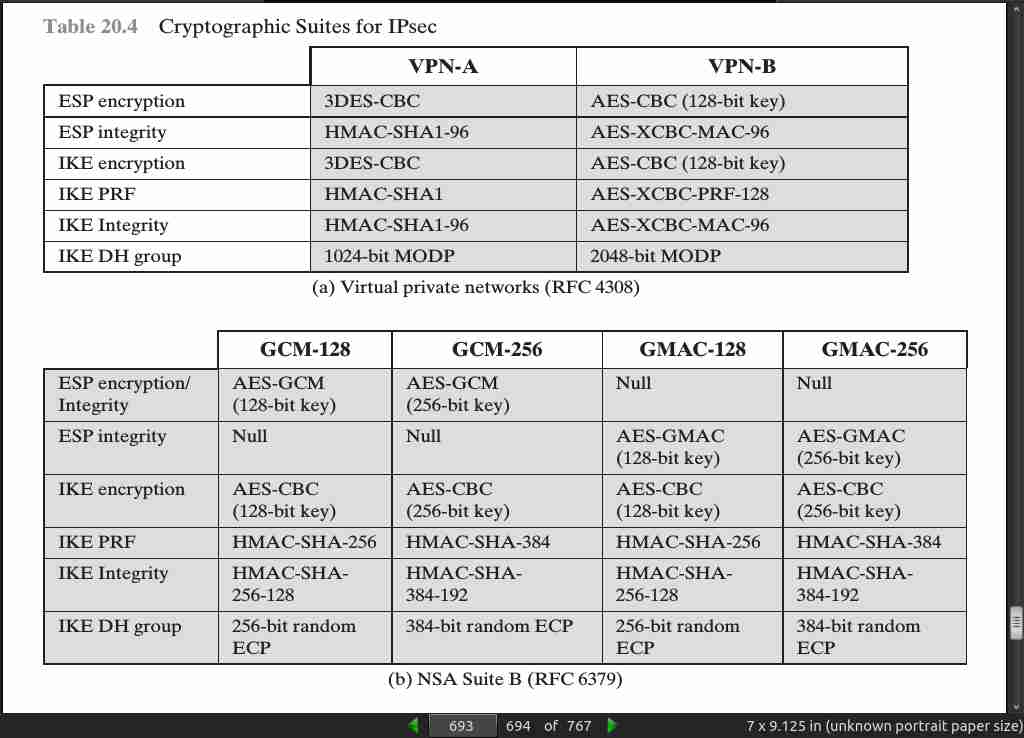
page 693:

• RFC 6379 defines four optional cryptographic suites that are compatible with the United States National Security Agency’s Suite B specifications. In 2005, the NSA issued Suite B, which defined the algorithms and strengths needed to protect both sensitive but unclassified (SBU) and classified information for use in its Cryptographic Modernization program [LATT09]. The four suites defined in RFC 6379 provide choices for ESP and IKE. The four suites are differentiated by the choice of cryptographic algorithm strengths and a choice of whether ESP is to provide both confidentiality and integrity or integrity only. All of the suites offer greater protection than the two VPN suites defined in RFC 4308.